题目内容
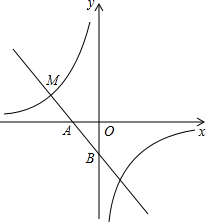 (2013•东城区二模)如图,一次函数y=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=
(2013•东城区二模)如图,一次函数y=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)若点P是反比例函数y=
| k |
| x |
分析:(1)将M坐标代入一次函数解析式求出m的值,确定出M坐标,将M坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)对于一次函数,分别令x与y为0求出A与B坐标,确定出三角形AOB面积,根据面积的关系求出三角形BOP的面积,由BO的长,利用面积公式求出P的横坐标,代入反比例解析式即可求出纵坐标,确定出满足题意得P坐标.
(2)对于一次函数,分别令x与y为0求出A与B坐标,确定出三角形AOB面积,根据面积的关系求出三角形BOP的面积,由BO的长,利用面积公式求出P的横坐标,代入反比例解析式即可求出纵坐标,确定出满足题意得P坐标.
解答:解:(1)∵M(-2,m)在一次函数y=-x-1的图象上,
∴m=2-1=1,
∴M(-2,1),
又M(-2,1)在反比例函数y=
图象上,
∴k=-2,
∴y=-
;
(2)由一次函数y=-x-1,令x=0,求出y=-1;令y=0求出x=-1,
∴A(-1,0),B(0,-1),即OA=OB=1,
∴S△AOB=
•|OA|•|OB|=
,
∴S△BOP=2△AOB=1,
设△BOP边OB上的高位h,则h=2,
则P点的横坐标为±2,
把P点的横坐标为±2代入y=-
,
可得P点的纵坐标为-1或1,
∴P(2,-1)或P(-2,1).
∴m=2-1=1,
∴M(-2,1),
又M(-2,1)在反比例函数y=
| k |
| x |
∴k=-2,
∴y=-
| 2 |
| x |
(2)由一次函数y=-x-1,令x=0,求出y=-1;令y=0求出x=-1,
∴A(-1,0),B(0,-1),即OA=OB=1,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BOP=2△AOB=1,
设△BOP边OB上的高位h,则h=2,
则P点的横坐标为±2,
把P点的横坐标为±2代入y=-
| 2 |
| x |
可得P点的纵坐标为-1或1,
∴P(2,-1)或P(-2,1).
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,一次函数与坐标轴的交点,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E.
(2013•东城区二模)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E. (2013•东城区二模)如图,在平面直角坐标系中,已知⊙O的半径为1,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
(2013•东城区二模)如图,在平面直角坐标系中,已知⊙O的半径为1,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )