题目内容
如图，在正方形ABCD中，E、F分别是AB和AD上的点，已知CE⊥BF，垂足为M，请找出图中和BE相等的线段，并说明你的结论.
和BE相等的线段是AF.理由见解析
解：和BE相等的线段是AF.理由如下：
因为ABCD是正方形，所以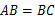
，∠
.
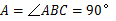因为CE⊥BF，所以∠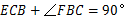
.
又因为∠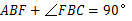
，
所以∠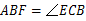
.
在△AFB和△BEC中，
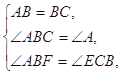
所以△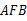
≌△
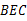，所以
.
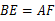因为ABCD是正方形，所以
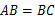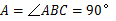，∠.因为CE⊥BF，所以∠
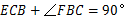.又因为∠
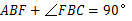，所以∠
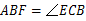.在△AFB和△BEC中，
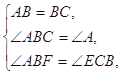
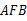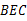所以△
≌△，所以.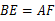
练习册系列答案
相关题目
D中，
∥
.
，
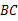，梯形的高是4，求梯形的周长；
，
，梯形的高是h，梯形的周长为c，请用
表示c；
，
，
.求证：
⊥
.
中，
⊥
于点
，
⊥
于点
.若
，
，且□
，
，则图中阴影部分的面积为（ ）