题目内容
已知在等腰梯形 D中,
D中, ∥
∥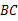 .
.
(1)若 ,
, ,梯形的高是4,求梯形的周长;
,梯形的高是4,求梯形的周长;
(2)若 ,
, ,梯形的高是h,梯形的周长为c,请用
,梯形的高是h,梯形的周长为c,请用 表示c;
表示c;
(3)若 ,
, ,
,
 .求证:
.求证: ⊥
⊥ .
.
 D中,
D中, ∥
∥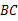 .
.(1)若
 ,
, ,梯形的高是4,求梯形的周长;
,梯形的高是4,求梯形的周长;(2)若
 ,
, ,梯形的高是h,梯形的周长为c,请用
,梯形的高是h,梯形的周长为c,请用 表示c;
表示c;(3)若
 ,
, ,
,
 .求证:
.求证: ⊥
⊥ .
.(1)26 (2)c= (3)见解析
(3)见解析
 (3)见解析
(3)见解析(1) 解:如图,作DE∥AB,DF⊥BC.

因为AD∥BC ,所以四边形ABED是平行四边形,
所以AB=DE,AD=BE.
因为AB=CD,所以DE=DC.
又DF⊥BC,所以EF=FC.
因为AD=5,BC=11, 梯形的高是4,
所以EC=BC-AD=6,EF=FC=3,DF=4,
从而 ,
,
梯形的周长为AB+BC+CD+AD=5+11+5+5=26.
(2) 解:若AD=a,BC=b,梯形的高是h,则DF=h,EF=FC= (b-a),
(b-a), .
.
所以梯形的周长c=AB+BC+CD+AD= .
.
(3)证明:如图,过点D作AC的平行线,交BC的延长线于点E.

由等腰梯形的性质得AC=BD.因为AD∥BC, ED∥AC,
所以四边形ACED是平行四边形,
所以AD=CE,AC=DE,从而BD=DE= .
.
又BE=BC+CE=BC+AD=10,
所以 ,
,
所以DE⊥BD,即AC⊥BD.

因为AD∥BC ,所以四边形ABED是平行四边形,
所以AB=DE,AD=BE.
因为AB=CD,所以DE=DC.
又DF⊥BC,所以EF=FC.
因为AD=5,BC=11, 梯形的高是4,
所以EC=BC-AD=6,EF=FC=3,DF=4,
从而
 ,
,梯形的周长为AB+BC+CD+AD=5+11+5+5=26.
(2) 解:若AD=a,BC=b,梯形的高是h,则DF=h,EF=FC=
 (b-a),
(b-a), .
.所以梯形的周长c=AB+BC+CD+AD=
 .
.(3)证明:如图,过点D作AC的平行线,交BC的延长线于点E.

由等腰梯形的性质得AC=BD.因为AD∥BC, ED∥AC,
所以四边形ACED是平行四边形,
所以AD=CE,AC=DE,从而BD=DE=
 .
.又BE=BC+CE=BC+AD=10,
所以
 ,
,所以DE⊥BD,即AC⊥BD.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目


 米,渠底与渠腰的夹角∠
米,渠底与渠腰的夹角∠ 120°,渠腰
120°,渠腰 米,求水渠的上口AD的长.
米,求水渠的上口AD的长.

 ,
, ,则梯形两腰中点的连线EF的长是( )
,则梯形两腰中点的连线EF的长是( )


 ,宽为
,宽为 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,将剪下的部分打开,得到的菱形的面积为( )
的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,将剪下的部分打开,得到的菱形的面积为( )



