题目内容
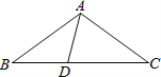
【题目】(1)如图,点C把线段AB分成两条线段AC和BC,如果![]() ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比。
,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比。
![]()
(2)已知:如图,已知△ABC∽△DEF,
求证:相似三角形面积的比等于相似比的平方

【答案】(1).![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)设AC=a,BC=b,由题意列式,整理得出关于![]() 的一元二次方程,令
的一元二次方程,令![]() =t,解关于t的一元二次方程即可;(2)作AG⊥BC交BC于点G,作DH⊥EF交EF于点H,设两个三角形的相似比为k,由已知条件不难证明△ABG∽△DEH,从而得出AG与DH的比值,再根据三角形面积公式列式计算出△ABC与△DEF的面积之比即可.
=t,解关于t的一元二次方程即可;(2)作AG⊥BC交BC于点G,作DH⊥EF交EF于点H,设两个三角形的相似比为k,由已知条件不难证明△ABG∽△DEH,从而得出AG与DH的比值,再根据三角形面积公式列式计算出△ABC与△DEF的面积之比即可.
(1)设AC=a,BC=b,
则![]() =
=![]() ,整理可得a2﹣ab﹣b2=0,
,整理可得a2﹣ab﹣b2=0,
∴![]() 2﹣
2﹣![]() ﹣1=0,
﹣1=0,
令![]() =t,t2﹣t﹣1=0,
=t,t2﹣t﹣1=0,
解得t=![]() (负值舍去),
(负值舍去),
∴t=![]() ,
,
∴黄金比为![]() ;
;
(2)证明:作AG⊥BC交BC于点G,作DH⊥EF交EF于点H,设两个三角形的相似比为k,
∴∠AGB=∠DHE=90°,
∵△ABC∽△DEF,
∴![]() =
=![]() =k,∠B=∠E,
=k,∠B=∠E,
∴△ABG∽△DEH,
∴![]() =
=![]() =k,
=k,
∴![]() =
=![]() =k2.
=k2.

练习册系列答案
相关题目