题目内容
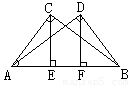
已知如图,AC=BC,∠C=90°,∠A的平分线AD交BC于D,过B作BE垂直AD于E,求证:BE= AD.
AD.
 解:如图,延长AC、BE交于点M,
解:如图,延长AC、BE交于点M,∵∠A的平分线AD,BE垂直AD于E,
∴∠MAE=∠BAE,∠AEM=∠AEB=90°,
∵AE=AE,
∴△AEM≌△AEB(ASA),
∴EM=BE,即BM=2BE①;
∵∠A的平分线AD,AC=BC,∠C=90°,
∴∠CAD=∠DAB=22.5°,∠ABC=45°,
∵BE垂直AD于E,
∴∠DAB+∠ABC+∠DBE=90°,即∠DBE=22.5°,
∴∠CAD=∠DBE,
又∵AC=BC,且∠ACB=∠BCM=90°,
∴△ACD≌△BCM(ASA),
∴AD=BM②;
由①②得AD=2BE,
即BE=
 AD.
AD.分析:延长AC、BE交于点M,易证得△ACD≌△BCM,可得AD=BM①,可证得△AEM≌△AEB,可得EM=BE,即BM=2BE②,由①②即可得结论.
点评:本题主要考查了全等三角形的判定和性质,涉及到等腰直角三角形的性质、三角形内角和定理等知识点,正确作出辅助线是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
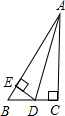 已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )| A、BD+ED=BC | B、DE平分∠ADB | C、AD平分∠EDC | D、ED+AC>AD |

 已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段
已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段