题目内容
已知如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E、F,求证:CE=DF.
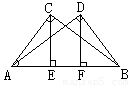
【答案】
见解析
【解析】
试题分析:先根据AD=BC及公共边AB,由“HL”证得Rt△ACB≌Rt△BDF,可得∠CAB=∠DBA,AC=BD,再根据“AAS”证得△CAE≌△BDF,问题得证。
在Rt△ACB与Rt△ABD中

∴Rt△ACB≌Rt△BDF(HL)
∴∠CAB=∠DBA,AC=BD
∴在Rt△CAE与Rt△BDF中

∴△CAE≌△BDF(AAS)
∴CE=DF.
考点:本题考查的是直角三角形的判定和性质
点评:本题中前后两次判定三角形全等,找到两次全等的连接点是解答本题的关键。

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
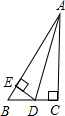 已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )| A、BD+ED=BC | B、DE平分∠ADB | C、AD平分∠EDC | D、ED+AC>AD |

 已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段
已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段 AD.
AD.