题目内容
已知△ABC和△BEF都是等边三角形
(1)如图1所示若AE=4cm,求CF的长;
(2)将图1△BEF顺时针旋转,使BF落在BA边上,如图2所示BC上取点D使CD=BE,连接DE,求证:∠EDB=∠CAD.
(1)如图1所示若AE=4cm,求CF的长;
(2)将图1△BEF顺时针旋转,使BF落在BA边上,如图2所示BC上取点D使CD=BE,连接DE,求证:∠EDB=∠CAD.

考点:全等三角形的判定与性质
专题:
分析:(1)易证△EBA≌△FBC,即可求得CF=AE,即可解题;
(2)作DG∥AB交AC于G,易证∠EBD=∠AGD和BD=AG,即可求证△ADG≌△DEB,即可解题.
(2)作DG∥AB交AC于G,易证∠EBD=∠AGD和BD=AG,即可求证△ADG≌△DEB,即可解题.
解答:解:(1)∵∠ABE=∠EBF+∠ABF,∠CBF=∠ABC+∠ABF,∠EBF=∠ABC,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(SAS),
∴CF=AE=4cm;
(2)作DG∥AB交AC于G,

∵DG∥AB,
∴∠ABD=∠GDC=60°,∠BAC=∠DGC=60°,
∵∠C=60°,
∴△CDG为等边三角形,
∴CD=CG=DG=BE,
∴BD=AG,
∵∠EBD=∠EBF+∠ABD=120°,∠AGD=180°-∠DGC=120°,
∴∠EBD=∠AGD,
在△ADG和△DEB中,
,
∴△ADG≌△DEB(SAS),
∴∠EDB=∠CAD.
∴∠ABE=∠CBF,
在△ABE和△CBF中,
|
∴△ABE≌△CBF(SAS),
∴CF=AE=4cm;
(2)作DG∥AB交AC于G,

∵DG∥AB,
∴∠ABD=∠GDC=60°,∠BAC=∠DGC=60°,
∵∠C=60°,
∴△CDG为等边三角形,
∴CD=CG=DG=BE,
∴BD=AG,
∵∠EBD=∠EBF+∠ABD=120°,∠AGD=180°-∠DGC=120°,
∴∠EBD=∠AGD,
在△ADG和△DEB中,
|
∴△ADG≌△DEB(SAS),
∴∠EDB=∠CAD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中找出全等三角形并求证是解题的关键.

练习册系列答案
相关题目
 如图,AB是半圆O的直径,点C是半圆O的二等分点,且弦CD=BD,连接OD、AD、AC,则AC与OD的位置关系是
如图,AB是半圆O的直径,点C是半圆O的二等分点,且弦CD=BD,连接OD、AD、AC,则AC与OD的位置关系是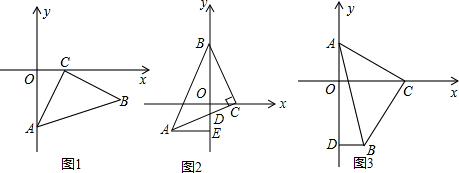
 如图,在长方形ABCD中,AB=2x+1,AE=5x-3,BF=3x+5,AD=6x+7,请以含x的多项式表示图中阴影部分的面积.
如图,在长方形ABCD中,AB=2x+1,AE=5x-3,BF=3x+5,AD=6x+7,请以含x的多项式表示图中阴影部分的面积.