题目内容
如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连结AC,DB.设CP=x,PD=y.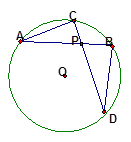
(1)求证:△ACP∽△DBP;
(2)求y关于x的函数解析式;
(3)若CD=8时,求S△ACP:S△DBP的值.
(1)见解析(2)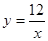 (3)S△ACP:S△DBP=4:9或4:1
(3)S△ACP:S△DBP=4:9或4:1
解析试题分析:(1)∵∠A=∠D, ∠C=∠B ∴△ACP∽△DBP
(2)由(1)得CP:BP=AP:PD即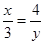 得
得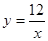
(3)由CD=8即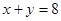 和
和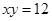 解得
解得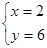 或
或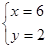
则S△ACP:S△DBP=4:9或4:1
考点:圆周角定理,根据实际问题列反比例函数关系式,相似三角形的判定
点评:难度系数中等,是代数几何综合题,需要熟悉相似三角形的判定,数形结合,综合运用。

练习册系列答案
相关题目
 如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连接AC,DB.设CP=x,PD=y.
如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连接AC,DB.设CP=x,PD=y. (2011•南岗区一模)如图,在△ABC中,⊙O经过点A、B,分别与边AC、BC相交于点D、E,且AD=BE,连接CO,求证:∠ACO=∠BCO.
(2011•南岗区一模)如图,在△ABC中,⊙O经过点A、B,分别与边AC、BC相交于点D、E,且AD=BE,连接CO,求证:∠ACO=∠BCO.

