题目内容
如图所示，AB是⊙O的一条弦，且OD⊥AB于点C，弧BD所对的圆周角∠DEB=35°，则∠AOD的度数是
- A.35°
- B.55°
- C.70°
- D.110°
C
分析：连接OB，由∠DEB=35°，推出∠DOB=70°，然后根据垂径定理即可推出∠AOD=∠DOB=70°．
解答：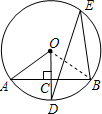
解：如图，连接OB．
∵∠DEB=35°，
∴∠DOB=70°．
又∵OD⊥AB，
∴∠AOD=∠DOB=70°．
故选C．
点评：本题考查了圆周角定理和垂径定理．圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
分析：连接OB，由∠DEB=35°，推出∠DOB=70°，然后根据垂径定理即可推出∠AOD=∠DOB=70°．
解答：
解：如图，连接OB．∵∠DEB=35°，
∴∠DOB=70°．
又∵OD⊥AB，
∴∠AOD=∠DOB=70°．
故选C．
点评：本题考查了圆周角定理和垂径定理．圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
全能测控一本好卷系列答案
相关题目
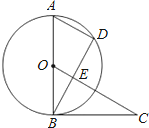如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A．
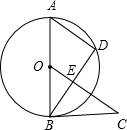如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A，OC⊥BD于点E．
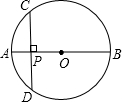如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，则⊙O的半径为
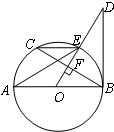如图所示，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，且∠AEC=∠ODB．
如图所示，AB是⊙O直径，∠D=35°，则∠BOC等于（ ）