题目内容
19.先化简($\frac{x-1}{{x}^{2}-4}$-$\frac{1}{x+2}$)÷$\frac{x}{{x}^{2}-2x}$,再选取一个你喜欢的x值求值.分析 先将题目中的式子化简,然后选取一个合适的值代入即可解答本题,注意x不能等于-2、2、0.
解答 解:($\frac{x-1}{{x}^{2}-4}$-$\frac{1}{x+2}$)÷$\frac{x}{{x}^{2}-2x}$
=$\frac{x-1-(x-2)}{(x+2)(x-2)}×\frac{x(x-2)}{x}$
=$\frac{1}{(x+2)(x-2)}×\frac{x(x-2)}{x}$
=$\frac{1}{x+2}$,
当x=1时,
原式=$\frac{1}{1+2}=\frac{1}{3}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.二次函数y=(x+1)2-4的顶点坐标是( )
| A. | (-1,-4) | B. | (1,4) | C. | (1,-4) | D. | (-1,4) |
11.若有理数a,b满足|a-1|+(b-2)2=0,则ab=( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
8.已知$\frac{a}{b}=\frac{7}{5}$,则$\frac{a-b}{b}$的值为( )
| A. | $\frac{2}{7}$ | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
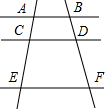 如图,AB∥CD∥EF,若$\frac{AC}{CE}$=$\frac{1}{2}$,则$\frac{BD}{BF}$=$\frac{1}{3}$.
如图,AB∥CD∥EF,若$\frac{AC}{CE}$=$\frac{1}{2}$,则$\frac{BD}{BF}$=$\frac{1}{3}$.