题目内容
7. 如图,⊙O的半径是4,AB是⊙O的弦,点P是弦AB上的动点,且2≤OP≤4,则弦AB所对的圆周角的度数是( )
如图,⊙O的半径是4,AB是⊙O的弦,点P是弦AB上的动点,且2≤OP≤4,则弦AB所对的圆周角的度数是( )| A. | 60° | B. | 120° | C. | 60°或120° | D. | 30°或150° |
分析 作OD⊥AB,如图,利用垂线段最短得OD=1,则根据含30度的直角三角形三边的关系得∠OAB=30°,根据三角形内角和定理可计算出∠AOB=120°,则可根据圆周角定理得到∠AEB=$\frac{1}{2}$∠AOB=60°,根据圆内接四边形的性质得∠F=120°,求出弦AB所对的圆周角的度数.
解答 解:作OD⊥AB,
∵点P是弦AB上的动点,且1≤OP≤2,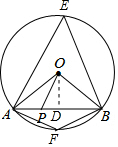
∴OD=1,
∴∠OAB=30°,
∴∠AOB=120°,
∴∠AEB=$\frac{1}{2}$∠AOB=60°,
∵∠E+∠F=180°,
∴∠F=120°,
即弦AB所对的圆周角的度数为60°或120°,
故选:C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
17.下列说法不正确的是( )
| A. | 调查一架“歼20”隐形战机各零部件的质量,应采用抽样调查 | |
| B. | 一组数据2,2,3,3,3,4的众数是3 | |
| C. | 如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是7 | |
| D. | 一组数据1,2,3,4,5的方差是2,那么数据11,12,13,14,15的方差也是2 |
15.-9的相反数是( )
| A. | 9 | B. | -9 | C. | -$\frac{1}{9}$ | D. | $\frac{1}{9}$ |
2.在正方形,矩形,菱形,平行四边形,正五边形五个图形中,中心对称图形的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12. 如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2的度数为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2的度数为( )
 如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2的度数为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2的度数为( )| A. | 54° | B. | 63° | C. | 72° | D. | 82° |
19. 中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中,
中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中, 所在位置的坐标为(-3,1),
所在位置的坐标为(-3,1), 所在位置的坐标为(2,-1),那么,
所在位置的坐标为(2,-1),那么, 所在位置的坐标为( )
所在位置的坐标为( )
 中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中,
中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中, 所在位置的坐标为(-3,1),
所在位置的坐标为(-3,1), 所在位置的坐标为(2,-1),那么,
所在位置的坐标为(2,-1),那么, 所在位置的坐标为( )
所在位置的坐标为( )| A. | (0,1) | B. | (4,0) | C. | (-1,0) | D. | (0,-1) |
16.今年参加菏泽市初中毕业学业水平考试的考生约有71000人,请将数字71000用科学记数法表示为( )
| A. | ×103 | B. | 7.1×104 | C. | 0.71×105 | D. | 71×103 |
17.为了了解某班学生每天使用零花钱的情况,班主任随机调查了15名同学,调查的结果如下表:
对于表中数据,下列说法正确的是( )
| 人数 | 1 | 3 | 5 | 4 | 2 |
| 每天零花钱(元) | 0 | 1 | 3 | 4 | 5 |
| A. | 中位数是3元 | B. | 平均数是2.5元 | C. | 方差是4 | D. | 众数是5元 |