题目内容
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿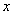 轴正方
轴正方 向以每秒1个单位的速度运动,同时动点
向以每秒1个单位的速度运动,同时动点 C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为
C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为 秒。
秒。
(1)当点 C运动到线段OB的中点时,求
C运动到线段OB的中点时,求 的值及点E的坐标;
的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
 (3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中,设□PCOD的面积为S。
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中,设□PCOD的面积为S。
①当点M,N中,有一点落在四边形ADEC的边上时,求出所有满足条件的 的值;
的值;
②若点M,N中恰好只有一个点落在四边形ADEC内部(不包括边界)时,直接写出S的取值范围。
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目



 B.
B.  C.
C.  D.
D. 


 的解是
的解是 
 个红球。
个红球。 ,求从袋中取出黑球的个数。
,求从袋中取出黑球的个数。 数为
数为
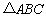 的三个顶点均在格点上,则
的三个顶点均在格点上,则 ( ).
( ). (B)
(B) (C)
(C) (D)
(D)

 方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45
方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向
方向 上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)