题目内容
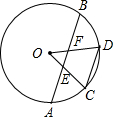 如图,在⊙O中,A、C、D、B是⊙O上四点,OC、OD交AB于E、F,且AE=BF.下列结论不正确的是( )
如图,在⊙O中,A、C、D、B是⊙O上四点,OC、OD交AB于E、F,且AE=BF.下列结论不正确的是( )| A、OE=OF | ||||
B、
| ||||
| C、AC=CD=DB | ||||
| D、CD∥AB |
考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:
分析:连接OA,OB,可以利用SAS判定△OAE≌△OBF,根据全等三角形的对应边相等,可得到OE=OF,判断A选项正确;由全等三角形的对应角相等,可得到∠AOE=∠BOF,即∠AOC=∠BOD,根据圆心角、弧、弦的关系定理得出
=
,判断B选项正确;连结AD.由
=
,根据圆周角定理得出∠BAD=∠ADC,则CD∥AB,判断D选项正确;由∠BOD=∠AOC不一定等于∠COD,得出弧AC=弧BD不一定等于弧CD,那么AC=BD不一定等于CD,判断C选项不正确.
 |
| AC |
 |
| BD |
 |
| AC |
 |
| BD |
解答: 解:连接OA,OB,
解:连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,
,
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴
=
,故B选项正确;
 连结AD.
连结AD.
∵
=
,
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴弧AC=弧BD不一定等于弧CD,
∴AC=BD不一定等于CD,
故C选项不正确.
故选C.
 解:连接OA,OB,
解:连接OA,OB,∵OA=OB,
∴∠OAB=∠OBA.
在△OAE与△OBF中,
|
∴△OAE≌△OBF(SAS),
∴OE=OF,故A选项正确;
∠AOE=∠BOF,即∠AOC=∠BOD,
∴
 |
| AC |
 |
| BD |
 连结AD.
连结AD.∵
 |
| AC |
 |
| BD |
∴∠BAD=∠ADC,
∴CD∥AB,故D选项正确;
∵∠BOD=∠AOC不一定等于∠COD,
∴弧AC=弧BD不一定等于弧CD,
∴AC=BD不一定等于CD,
故C选项不正确.
故选C.
点评:本题考查了全等三角形的判定与性质,圆心角、弧、弦的关系定理,圆周角定理,平行线的判定,难度适中.准确作出辅助线利用数形结合思想是解题的关键.

练习册系列答案
相关题目
下列等式不成立的是( )
A、
| ||
| B、(-2)3=-8 | ||
| C、-(-4)=4 | ||
| D、0×2009=2009 |
用配方法将a2-4a+5二次三项式变形,结果是( )
| A、(a-2)2+1 |
| B、(a+2)2-1 |
| C、(a-2)2-1 |
| D、(a+2)2+1 |
两个有理数和为0,积为负,则这两个数的关系是( )
| A、两个数均为0 |
| B、两个数中一个为0 |
| C、两数互为相反数 |
| D、两数互为相反数,但不为0 |
 如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是
如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是