题目内容
如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按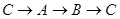 的路径运动,且速度为每秒2㎝,设运动的时间为t秒
的路径运动,且速度为每秒2㎝,设运动的时间为t秒
【小题1】当t为何值时,CP把△ABC的周长分成相等的两部分;
【小题2】当t为何值时,CP把△ABC的面积分成相等的两部分;并求此时CP的长
【小题3】当t为何值时,△BCP为等腰三角形?
【小题1】6
【小题2】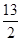
【小题3】6,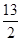 ,5.4,3.
,5.4,3.
解析在△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,由勾股定理得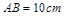 .
.
【小题1】此三角形的周长为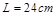 ,当CP把△ABC的周长分成相等的两部分时,点
,当CP把△ABC的周长分成相等的两部分时,点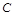 所以过的路程为
所以过的路程为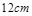 ,因运动速度为
,因运动速度为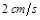 ,所以历的时间为
,所以历的时间为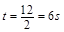 .
.
【小题2】若CP把△ABC的面积分成相等的两部分,则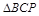 的面积等于
的面积等于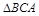 的一半;设
的一半;设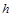 为
为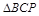 的高,则
的高,则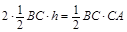 ,则
,则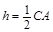 ,所以点
,所以点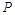 应为
应为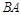 的中点,所以点运动的路程为
的中点,所以点运动的路程为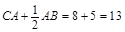 ,其运动时间为
,其运动时间为
【小题3】当△BCP为等腰三角形时,有以下几种情形:
情形之一:如图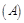 ,
, ,此时
,此时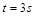 ;
;
情形之二:如图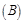 ,
,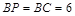 ,此时
,此时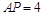 ,
,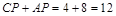 ,其时间为
,其时间为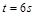 ;
;
情形之三:如图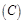 ,
,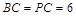 ,此时过点
,此时过点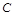 作
作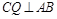 于点
于点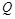 ,则
,则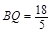 ,于是
,于是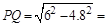
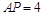 ,
,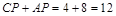 ,其时间为
,其时间为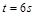 ;则
;则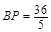 ,所以
,所以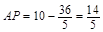 ,所以
,所以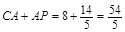 ,所以所经过的时间为
,所以所经过的时间为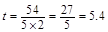
情形之四:如图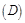 ,
,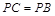 ,此时
,此时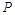 恰为
恰为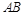 的中点,则
的中点,则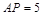 ,于是有
,于是有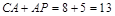 ,所以
,所以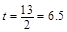
所以当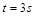 或
或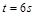 或
或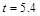 或
或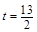 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.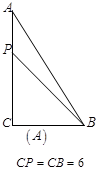
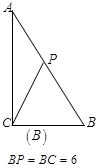
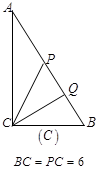
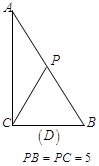

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.