Question

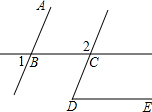如图，∠1=45°，∠2=135°，∠D=45°．AB与CD平行吗？为什么？BC与DE呢？
解：∵∠1=45°
∴∠1=∠________=45°．（________ ）
又∵∠2=135°，
∴________=180°
∴AB∥CD（________）
又∵∠2+∠3=180°（________）
∴∠3=________=________°（请在图中标出你确定的∠3）
又∵∠D=∠3=45°，
∴BC∥DE　（________）．

Answer 1

ABC    对顶角相等    ∠ABC+∠2    同旁内角互补，两直线平行    邻补角互补    180°-135°    45    内错角相等两直线平行
分析：首先根据∠1=45°可得∠ABC=45°，进而得到∠2和∠ABC互补，可证明AB∥CD，再根据邻补角互补可以计算出∠3的度数，进而得到∠D=∠3=45°，即可证明BC∥DE．
解答：解：∵∠1=45°，
∴∠1=∠ABC=45°．（ 对顶角相等 ）
又∵∠2=135°，
∴∠ABC+∠2=180°，
∴AB∥CD，（ 同旁内角互补，两直线平行）
又∵∠2+∠3=180°，（ 邻补角互补）
∴∠3=180°-135°=45°，
又∵∠D=∠3=45°，
∴BC∥DE． （ 内错角相等两直线平行）
点评：此题主要考查了平行线的判定与性质，关键是掌握平行线的判定定理与性质定理，注意区分这两种定理的不同，不要混淆．