��Ŀ����
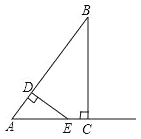
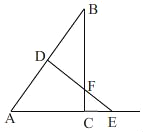
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=3��BC=4������D�ӵ�A������ÿ��3����λ���ٶ��˶�����B������D��DE��AB������AC�ڵ�E�����D���˶�ʱ��Ϊt�루t��0����
��1���߶�AE�ij�Ϊ�� �������ú�t�Ĵ���ʽ��ʾ��
��2������ADE����ACB�������Ϊ1��4ʱ����t��ֵ��
��3������ADE����ACB�ص�����ͼ�ε��ܳ�ΪL����L��t֮��ĺ�����ϵʽ��
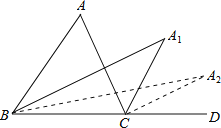
��4����ֱ��DE����ACB�ֳɵ�������ͼ������һ������Գ�ͼ��ʱ��ֱ��д��t��ֵ��
���𰸡���1��5t����2��![]() ����3����
����3����![]() ʱ��L=12t����
ʱ��L=12t����![]() ʱ��
ʱ�� ![]() ����4��
����4��![]() ��1��
��1��
���������������������1���������Ǻ����������2�����ݡ�ADE����ACB�������Ϊ1��4�г������������3������![]() ��
��![]() ������������� ��4����DE=CEʱ���ı���BCED����Գ�ͼ�Σ��͵�DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ��������������.
������������� ��4����DE=CEʱ���ı���BCED����Գ�ͼ�Σ��͵�DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ��������������.
�����������
��1����Rt��ABC��tanA=![]() =
=![]()
������ã�AD=3t��
��Rt��ADE��tanA=![]() =
=![]() =
=![]() ��
��
���ݹ��ɶ����ã�AE=5t��
�ʴ�Ϊ5t��
��2������һ����ED��AB��
���ADE=90�㣮�ߡ�ACB=90�㣬
���ACB=��ADE����A=��A��
���ABC�ס�AED��
��![]() ��
��
��AD=3t��AC=3��BC=4��
��DE=4t��
��![]() ��
��
��![]() ��
��
��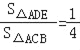 ��
��
��![]() ��
��
��![]() ���ᣩ
���ᣩ
��t��ֵΪ![]() ��
��
����������ED��AB��
���ADE=90�㣮
�ߡ�ACB=90�㣬
���ACB=��ADE��
�ߡ�A=��A��
���ABC�ס�AED��
��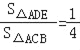 ��
��
��![]() ��
��
��AC=3��AD=3t��
��2��3t=3��t=![]() ��
��
��3���ɣ�2���ã���ABC�ס�AED��
��![]() ��
��
��AD=3t��
��DE=4t��AE=5t��BD=5��3t��
�൱![]() ʱ��L=3t+4t+5t=12t��
ʱ��L=3t+4t+5t=12t��
��L=12t��
��![]() ʱ����ͼ��
ʱ����ͼ��
�ߡ�B=��B����BDF=��BCA��
���ABC�ס�FBD��
��![]() ��
��
��BD=5��3t��
��![]() ��
��
�ߡ�BFD=��EFC����BDF=��ECF��
���B=��E��
�ߡ�FCE=��BCA
���BCA�ס�ECF��
��![]() ��
��
��CE=5t��3��
��![]() ��
��
![]() ��
��
��![]() ��
��
��4���ɣ�1��֪��AE=5t��DE=4t��
��CE=3��5t��
��DE=CEʱ���ı���BCED����Գ�ͼ�Σ�
��4t=3��5t��
��t=![]() ��
��
��DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ�Σ�
��AD=3t��AC=3��
��3t=3��
��t=1��
��������������ʱ��tΪ![]() ��1��
��1��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����ʮһ���ƽ���,��ʤ�ҵ�Ǵ�������,�������һֱ����![]() �±�Ϊ������ǰһ���Ӫҵ����ǵ����
�±�Ϊ������ǰһ���Ӫҵ����ǵ����![]() ��֪9��30�յ�Ӫҵ��Ϊ26��Ԫ��
��֪9��30�յ�Ӫҵ��Ϊ26��Ԫ��
10��1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
4 | 3 | 2 | 0 |
|
|
|
![]() �ƽ�����������͵���һ�죿
�ƽ�����������͵���һ�죿![]() ֱ�ӻش�,����д����
ֱ�ӻش�,����д����![]() ��
��
![]() �ƽ�����ƽ��ÿ���Ӫҵ���Ƕ��٣�
�ƽ�����ƽ��ÿ���Ӫҵ���Ƕ��٣�