题目内容
定义:设x为实数,[x]表示不大于x的最大整数,称为x的整数部分,{x}=x-[x]称为x的小数部分.试解方程:[x]-3{x}=2.分析:原方程化为[x]=2+3{x},0<{x}<1,从而可得3{x}为整数,这样即可得出{x}的值及[x]的值,继而得出方程的解.
解答:解:∵[x]表示不大于x的最大整数,{x}=x-[x]称为x的小数部分,
∴0≤{x}<1,
原方程化为[x]=2+3{x},
则可得2+3{x}是正整数,即可得3{x}为整数,
∴{x}=0或
或
,
①当{x}=0时,[x]=2,此时x=2;
②当{x}=
时,[x]=3,此时x=
;
③当{x}=
时,[x]=4,此时x=
;
综上可得方程[x]-3{x}=2的解为x=2或x=
或x=
.
∴0≤{x}<1,
原方程化为[x]=2+3{x},
则可得2+3{x}是正整数,即可得3{x}为整数,
∴{x}=0或
| 1 |
| 3 |
| 2 |
| 3 |
①当{x}=0时,[x]=2,此时x=2;
②当{x}=
| 1 |
| 3 |
| 10 |
| 3 |
③当{x}=
| 2 |
| 3 |
| 14 |
| 3 |
综上可得方程[x]-3{x}=2的解为x=2或x=
| 10 |
| 3 |
| 14 |
| 3 |
点评:本题考查了取整函数的知识,根据题意得出0≤{x}<1及3{x}为整数是解答本题的关键,比较抽象,难度较大,注意分类讨论{x}的值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;
个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;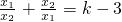 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由. 个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;
个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点; 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.