题目内容
 如图所示,点A(3,n)是反比例函数y=-
如图所示,点A(3,n)是反比例函数y=-| 6 |
| x |
| 6 |
| x |
(7,-
)或(-1,6)
| 6 |
| 7 |
(7,-
)或(-1,6)
.| 6 |
| 7 |
分析:首先利用解析式求出A点坐标,进而得出AB的长度,再利用图形表示出△APB的面积,进而求出即可.
解答: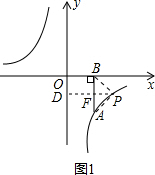 解:∵点A(3,n)是反比例函数y=-
解:∵点A(3,n)是反比例函数y=-
图象上的一点,
∴n=-
=-2,
∴A点坐标为:(3,-2),
如图1,过点P作PD⊥y轴于点D,交AB于点F,设P点坐标为(x,-
),
∵S△ABP=4,
∴
×AB•PF=4,
即
×2×(x-3)=4,
解得:x=7,
故P点坐标为:(7,-
),
如图2,过点P作PE⊥AB于点E,设P点坐标为(a,-
),
∵S△ABP=4,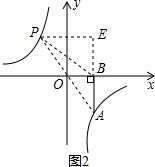
∴
×AB•PE=4,
即
×2×(3-a)=4,
解得:a=-1,
故P点坐标为:(-1,6),
故P点的坐标是:(7,-
)或(-1,6),
故答案为:(7,-
)或(-1,6).
 解:∵点A(3,n)是反比例函数y=-
解:∵点A(3,n)是反比例函数y=-| 6 |
| x |
∴n=-
| 6 |
| 3 |
∴A点坐标为:(3,-2),
如图1,过点P作PD⊥y轴于点D,交AB于点F,设P点坐标为(x,-
| 6 |
| x |
∵S△ABP=4,
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
解得:x=7,
故P点坐标为:(7,-
| 6 |
| 7 |
如图2,过点P作PE⊥AB于点E,设P点坐标为(a,-
| 6 |
| a |
∵S△ABP=4,

∴
| 1 |
| 2 |
即
| 1 |
| 2 |
解得:a=-1,
故P点坐标为:(-1,6),
故P点的坐标是:(7,-
| 6 |
| 7 |
故答案为:(7,-
| 6 |
| 7 |
点评:此题主要考查了反比例函数y=
中k的几何意义以及三角形面积求法,利用数形结合正确表示出△APB的面积是解题关键.
| k |
| x |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
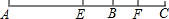
 11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形ABCD的边长为4,FG=3,FP=1,则△DEK的面积为
11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形ABCD的边长为4,FG=3,FP=1,则△DEK的面积为 8、正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为( )
8、正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为( ) (2012•鄂州)在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为( )
(2012•鄂州)在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为( ) 如图所示,点C在线段BE上,在BE同侧作等边△ABC和等边△DCE,那么,从旋转的角度我们可以看到,△ACE旋转后与△BCD重合.
如图所示,点C在线段BE上,在BE同侧作等边△ABC和等边△DCE,那么,从旋转的角度我们可以看到,△ACE旋转后与△BCD重合.