题目内容
已知抛物线y=ax2+bx-1经过点A(一1,0)、B(m,0)(m>0),且与y轴交于点C
(1)求抛物线对应的函数表达式(用含m的式子表示);
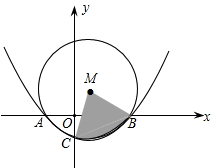
(2)如图,⊙M经过A、B、C三点,求扇形MBC(阴影部分)的面积S(用含m的式子表示);
(3)若抛物线上存在点P,使得△APB∽△ABC,求m的值.
(1)求抛物线对应的函数表达式(用含m的式子表示);
(2)如图,⊙M经过A、B、C三点,求扇形MBC(阴影部分)的面积S(用含m的式子表示);
(3)若抛物线上存在点P,使得△APB∽△ABC,求m的值.

(1)∵点(-1,0)、(m,0)在抛物线y=ax2+bx-1上
∴
,
解得
∴抛物线对应的函数表达式为:y=
x2+
x-1.
(2)在抛物线对应的函数表达式中,令x=0,得y=-1,
∴点C坐标为(0,-1).
∴OA=OC,
∴∠OAC=45°,
∴∠BMC=2∠OAC=90°.
又∵BC=
,∴MB=MC=
BC.
∴S=
π•MB2=
π•(
BC)2=
BC2=
.
(3)如图,∵△ABC∽△APB,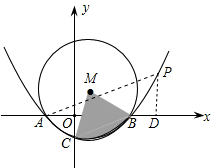
∴∠PAB=∠BAC=∠45°,
=
,
过点P作PD⊥x轴,垂足为D,连接PA、PB,
在Rt△PDA中,
∵∠PAB=∠APD=45°,
∴PD=AD,
设点P坐标为(x,x+1),
∵点P在抛物线上,
∴x+1=
x2+
x-1,即x2+(1-2m)x-2m=0,
解得x1=-1,x2=2m,
∴P1(2m,2m+1),P2(-1,0)(不合题意,舍去),
此进AP=
PD=(2m+1)
,又由
=
,得AC•AP=AB2,
则
(2m+1)
=(m+1)2,整理,得m2-2m-1=0,
解得m1=1+
,m2=1-
(舍去),
m的值是1+
.
∴
|
解得
|
∴抛物线对应的函数表达式为:y=
| 1 |
| m |
| 1-m |
| m |
(2)在抛物线对应的函数表达式中,令x=0,得y=-1,
∴点C坐标为(0,-1).
∴OA=OC,
∴∠OAC=45°,
∴∠BMC=2∠OAC=90°.
又∵BC=
| m2+1 |
| ||
| 2 |
∴S=
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| π |
| 8 |
| (m2+1)π |
| 8 |
(3)如图,∵△ABC∽△APB,

∴∠PAB=∠BAC=∠45°,
| AB |
| AP |
| AC |
| AB |
过点P作PD⊥x轴,垂足为D,连接PA、PB,
在Rt△PDA中,
∵∠PAB=∠APD=45°,
∴PD=AD,
设点P坐标为(x,x+1),
∵点P在抛物线上,
∴x+1=
| 1 |
| m |
| 1-m |
| m |
解得x1=-1,x2=2m,
∴P1(2m,2m+1),P2(-1,0)(不合题意,舍去),
此进AP=
| 2 |
| 2 |
| AB |
| AP |
| AC |
| AB |
则
| 2 |
| 2 |
解得m1=1+
| 2 |
| 2 |
m的值是1+
| 2 |

练习册系列答案
相关题目






 似解.(结果保留两个有效数字)
似解.(结果保留两个有效数字)