题目内容
已知△ABC中,D为AB的中点,E为AC上一点,AE=2CE,CD,BE交于O点,OE=2厘米.求BO的长.
 解:在△ABC中,做DF∥AC,如图
解:在△ABC中,做DF∥AC,如图∵D为AB的中点,且DF∥AC.
∴F为BE的中点,即EF=FB.
∵DF∥AC,
∴∠DFO=∠OEC,∠OCE=∠ODF
∵DF为△ABE的中位线,∴DF=
 AE,
AE,又∵AE=2EC∴DF=EC.
∴△DFO≌△CEO,∴EO=FO,
∵BF=FE,
∴BO=3EO=3×2=6厘米.
分析:根据三角形中位线定理可得:DF=
 AE,再综合题目中已知条件,可以求证△DFO≌△CEO,全等三角形的对应边相等,即EO=FO,计算BO.
AE,再综合题目中已知条件,可以求证△DFO≌△CEO,全等三角形的对应边相等,即EO=FO,计算BO.点评:考查三角形中位线定理在三角形中的应用,考查全等三角形的证明.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
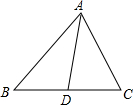 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
 25、阅读下面问题的解决过程:
25、阅读下面问题的解决过程:
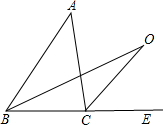
 (2014•宝山区一模)如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为
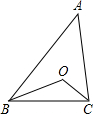
(2014•宝山区一模)如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 已知△ABC中,D为边BC上一点,AB=AD=CD,BE平分∠ABC,交AC于E点.
已知△ABC中,D为边BC上一点,AB=AD=CD,BE平分∠ABC,交AC于E点.