题目内容
【题目】函数![]() 、
、![]() 、
、![]() 都是常数,且
都是常数,且![]() 叫做“奇特函数”,当
叫做“奇特函数”,当![]() 时,奇特函数
时,奇特函数![]() 就成为反比例函数
就成为反比例函数![]() 是常数,且
是常数,且![]() .
.
![]() 若矩形的两边长分别是
若矩形的两边长分别是![]() 、
、![]() ,当两边长分别增加
,当两边长分别增加![]() 、
、![]() 后得到的新矩形的面积是
后得到的新矩形的面积是![]() ,求
,求![]() 与
与![]() 的函数关系式,并判断这个函数是否“奇特函数”;
的函数关系式,并判断这个函数是否“奇特函数”;
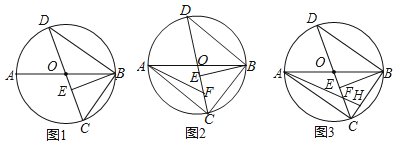
![]() 如图在直角坐标系中,点
如图在直角坐标系中,点![]() 为原点矩形
为原点矩形![]() 的顶点,
的顶点,![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() 、
、![]() 交于
交于![]() ,“奇特函数”
,“奇特函数”![]() 的图象经过点
的图象经过点![]() 、
、![]() ,求这个函数的解析式,并判断
,求这个函数的解析式,并判断![]() 、
、![]() 、
、![]() 三点是否在这个函数图象上;
三点是否在这个函数图象上;
![]() 对于
对于![]() 中的“奇特函数”
中的“奇特函数”![]() 的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.
的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.

【答案】![]() 根据新定义判断得出这个函数是“奇特函数”;
根据新定义判断得出这个函数是“奇特函数”;![]() 点不在这个函数图象上,
点不在这个函数图象上,![]() 点在这个函数图象上;
点在这个函数图象上;![]() 向左平移
向左平移![]() 个单位长度,向下平移
个单位长度,向下平移![]() 个单位长度,得到反比例函数
个单位长度,得到反比例函数![]() .
.
【解析】
(1)列出关于x和y的函数关系式后,看是否能整理成“奇特函数”的形式;
(2)分别求解出OB和CD所在直线的解析式,联立求解这两条直线的交点E点的坐标,再将E点和B点的坐标代入“奇特函数”求解其解析式,最后再分别代入![]() 、
、![]() 、
、![]() 三点进行验证即可;
三点进行验证即可;
(3)将“奇特函数”整理为![]() 的形式,再利用函数图像平移的规则即可.
的形式,再利用函数图像平移的规则即可.
![]() 由题意得:
由题意得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据新定义判断得出这个函数是“奇特函数”;
![]() 由题意得:点
由题意得:点![]() 的坐标是
的坐标是![]() ,
,
设直线![]() 解析式为
解析式为![]() ,则
,则![]() ,
,![]() ,
,
直线![]() 解析式为
解析式为![]() ,
,
∵点![]() 是
是![]() 中点,
中点,
∴点![]() 的坐标是
的坐标是![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
则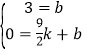 ,
,
解得:![]()
直线![]() 解析式为
解析式为![]() ,
,
由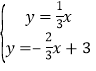 得:
得:![]() ,
,
则点![]() 的坐标是
的坐标是![]() ,
,
将![]() ,
,![]() 代入函数
代入函数![]() 得:
得:
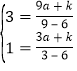 ,
,
解得:![]() ,
,
则“奇特函数”的解析式为![]() ,
,
∵把![]() 点的坐标
点的坐标![]() 代入得:
代入得:![]() ,∴
,∴![]() 点不在这个函数图象上,
点不在这个函数图象上,
∵把![]() 点的坐标
点的坐标![]() 代入得:
代入得:![]() ,∴
,∴![]() 点不在这个函数图象上,
点不在这个函数图象上,
∵把![]() 点的坐标
点的坐标![]() 代入得:
代入得: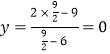 ,∴
,∴![]() 点在这个函数图象上;
点在这个函数图象上;
![]() ∵
∵![]() ,
,
∴向左平移![]() 个单位长度,向下平移
个单位长度,向下平移![]() 个单位长度,得到反比例函数
个单位长度,得到反比例函数![]() .
.

【题目】若二次函数![]() 的图象与
的图象与![]() 轴交于A、B两点(A点在B点左侧),顶点为
轴交于A、B两点(A点在B点左侧),顶点为![]() ,
,
(1)求A、B、![]() 三点坐标。
三点坐标。
(2)在平面直角坐标系中,用列表描点法,作出抛物线图象(如图),并根据图象回答,![]() 为何值时,函数值大于0?
为何值时,函数值大于0?
| |||||||
|
(3)将此抛物线向下平移2个单位,请写出平移后的解析式。