题目内容
已知:抛物线,对称轴为直线
,抛物线与y轴交于点
,与
轴交于
、
两点.
(1)求直线的解析式;
(2)若点是线段
下方抛物线上的动点,求四边形
面积的最大值;
(3)为抛物线上一点,若以线段
为直径的圆与直线
切于点
,求点
的坐标.
(1)
(2)
(3)
解析:解:(1)∵对称轴
∴ ……………………………………………………1分
∵
∴
设直线AC的解析式为
∵,
, 代入得:
直线的解析式为
………………………………………2分
(2)代数方法一:
过点D作DM∥y轴分别交线段AC和x轴于点M、N.
设,则
…………………………………3分
∵
……………………………………5分
∴当时,四边形ABCD面积有最大值
.
代数方法二:
=
= ……………………………………5分
∴当时,四边形ABCD面积有最大值
.
几何方法:
过点作
的平行线
,设直线
的解析式为
.
由得:
………………………………3分
当时,直线
与抛物线只有一个公共点
即:当时,△ADC的面积最大,四边形ABCD面积最大
此时公共点的坐标为
………………………………4分
= ………………………………5分
即:当时,四边形ABCD面积有最大值
.
(3)如图所示,由抛物线的轴对称性可求得(1,0)
∵以线段为直径的圆与直线
切于点
∴过点作
的垂线交抛物线于一点,则此点必为点
.
过点作
轴于点
, 可证Rt△PEB∽Rt△BOC
∴,故EB=3PE,……………………………………………………6分
设,
∵B(1,0)
∴BE=1-x,PE=
,
解得(不合题意舍去),
∴P点的坐标为: .………………………………………………7分

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案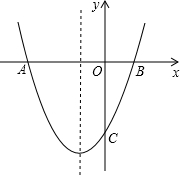 (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).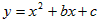 的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C。
的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C。 ,对称轴为直线
,对称轴为直线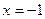 ,抛物线与y轴交于点
,抛物线与y轴交于点 ,与
,与 轴交于
轴交于 、
、 两点.
两点.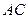 的解析式;
的解析式; 是线段
是线段 面积的最大值;
面积的最大值; 为抛物线上一点,若以线段
为抛物线上一点,若以线段 为直径的圆与直线
为直径的圆与直线 切于点
切于点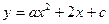 ,对称轴为直线
,对称轴为直线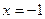 ,抛物线与y轴交于点
,抛物线与y轴交于点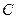 ,与
,与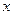 轴交于
轴交于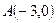 、
、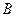 两点.
两点.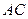 的解析式;
的解析式;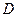 是线段
是线段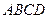 面积的最大值;
面积的最大值;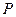 为抛物线上一点,若以线段
为抛物线上一点,若以线段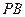 为直径的圆与直线
为直径的圆与直线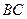 切于点
切于点