题目内容
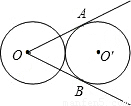
如图，两个等圆⊙O与⊙O′外切，过点O作⊙O′的两条切线OA、OB，A、B是切点，则∠AOB= 度．
【答案】分析：根据切线的性质得O′A⊥OA，再解直角三角形即可．
解答：
解：连接OO′和O′A，
根据切线的性质，得O′A⊥OA，
根据题意得OO′=2O′A，
则∠AOO′=30°，
再根据切线长定理得∠AOB=2∠AOO′=60°．
故答案是：60．
点评：本题综合运用了切线的性质定理、切线长定理以及借助锐角三角函数进行解答．
解答：
解：连接OO′和O′A，根据切线的性质，得O′A⊥OA，
根据题意得OO′=2O′A，
则∠AOO′=30°，
再根据切线长定理得∠AOB=2∠AOO′=60°．
故答案是：60．
点评：本题综合运用了切线的性质定理、切线长定理以及借助锐角三角函数进行解答．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
16、如图，两个等圆⊙O与⊙O′外切，过点O作⊙O′的两条切线OA、OB，A、B是切点，则∠AOB=
17、如图：两个等圆⊙A与⊙B外切，过A作⊙B的两条切线AC、AD，C、D是切点，则∠CAD=
