题目内容
13.下列各组中的两个分式是否相等?为什么?(1)$\frac{4a+b}{ab}$与$\frac{8{a}^{2}b+2a{b}^{2}}{2{a}^{2}{b}^{3}}$
(2)$\frac{{m}^{2}-3m}{9-{m}^{2}}$与$\frac{m-3}{m+3}$.
分析 (1)根据分式的基本性质进行变形判断即可;
(2)根据分式的基本性质进行变形判断即可.
解答 解:(1)$\frac{8{a}^{2}b+2a{b}^{2}}{2{a}^{2}{b}^{3}}$=$\frac{4a+b}{a{b}^{2}}$$≠\frac{4a+b}{ab}$;
(2)$\frac{{m}^{2}-3m}{9-{m}^{2}}=\frac{m(m-3)}{(3-m)(3+m)}=-\frac{m}{3+m}$$≠\frac{m-3}{m+3}$.
点评 本题考查了分式的性质,分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月.如果要保证该河段河沙不被开采枯竭,问最多可供多少人进行连续不间断的开采?(假定该河段河沙沉积的速度相对稳定)( )
| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
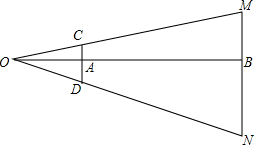 如图,小明家的窗口面对大楼,相距AB=80m,窗高CD=1.2m,小明从窗口后退2m,眼睛从点O处恰仔能看到楼顶M和楼底N,求大楼的高度.
如图,小明家的窗口面对大楼,相距AB=80m,窗高CD=1.2m,小明从窗口后退2m,眼睛从点O处恰仔能看到楼顶M和楼底N,求大楼的高度. 如图所示.在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
如图所示.在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.