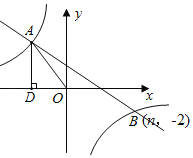
题目内容
【题目】已知![]() 为等腰
为等腰![]() 斜边
斜边![]() 上的两点,
上的两点,![]() ,
,![]() ,
,![]() .则
.则![]() ( )
( )
A.3B.![]() C.4D.
C.4D.![]()
【答案】C
【解析】
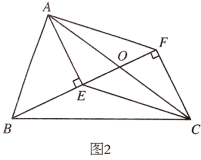
根据题意,画图如下,过点A作AG⊥AM,且AG=AM,连接CG和NG,利用SAS即可证出△BAM≌△CAG,从而得出CG=BM=3,∠ACG=∠B=45°,∠NCG=90°,然后利用SAS证出△MAN≌△GAN,可得MN=GN,设NC=x,利用勾股定理列出方程即可求出结论.
解:根据题意,画图如下,过点A作AG⊥AM,且AG=AM,连接CG和NG
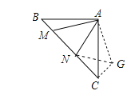
∵△ABC为等腰直角三角形,![]()
∴∠B=∠ACB=45°,∠BAC=90°,BC=![]()
∴∠BAM+∠MAC=90°,∠CAG+∠MAC=90°
∴∠BAM=∠CAG
在△BAM和△CAG中
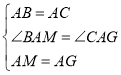
∴△BAM≌△CAG
∴CG=BM=3,∠ACG=∠B=45°
∴∠NCG=∠ACB+∠ACG=90°
∵![]()
∴∠GAN=∠MAG-∠MAN=45°
∴∠MAN=∠GAN
∵AM=AG,AN=AN
∴△MAN≌△GAN
∴MN=GN
设NC=x,则GN =MN= BC-BM-NC=9-x,
在Rt△NCG中,NC2+CG2=GN2
∴x2+32=(9-x)2
解得:x=4
即NC=4
故选C.

练习册系列答案
相关题目