题目内容
如果函数 y=(m+1)x+m2﹣1 是正比例函数.则 m 的值是 .
1 .
【考点】正比例函数的性质.
【分析】由正比例函数的定义:可得 m2﹣1=0,且 m+1≠0,然后解关于 m 的一元二次方程即可.
【解答】解:由正比例函数的定义可得:m2﹣1=0,且 m+1≠0, 解得,m=1;
故答案为:1.
【点评】此题主要考查了正比例函数的定义.解题关键是掌握正比例函数的定义条件:正比例函数
y=kx 的定义条件是:k 为常数且 k≠0,自变量次数为 1.

练习册系列答案
相关题目

 有意义时,函数 y=x+1 中 y 的取值范围是( )
有意义时,函数 y=x+1 中 y 的取值范围是( )
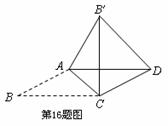
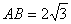 ,∠AB′D=75°,则BC = .
,∠AB′D=75°,则BC = .