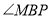题目内容
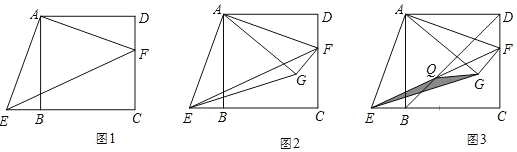
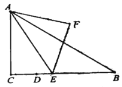
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .当点
.当点![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动的路径长为_________.
的运动的路径长为_________.
【答案】![]()
【解析】
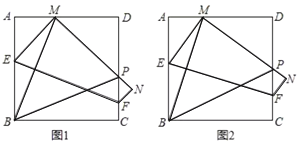
如图,连接CF,作FM⊥BC于M,FN⊥AC于N.证明△FNA≌△FME(AAS),推出FM=FM,AN=EM,推出四边形CMFN是正方形,推出点F在射线CF上运动(CF是∠ACB的角平分线),求出两种特殊位置CF的长即可解决问题.
如图,连接CF,作FM⊥BC于M,FN⊥AC于N.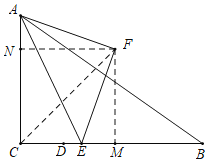
∵∠FNC=∠MCN=∠FMC=90°,
∴四边形CMFN是矩形,
∴∠MFN=∠AFE=90°,
∴∠AFN=∠MFE,
∵AF=FE,∠FNA=∠FME=90°,
∴△FNA≌△FME(AAS),
∴FM=FM,AN=EM,
∴四边形CMFN是正方形,
∴CN=CM,CF=![]() CM,∠FCN=∠FCM=45°,
CM,∠FCN=∠FCM=45°,
∵AC+CE=CN+AN+CM-EM=2CM,
∴CF=![]() (AC+CE).
(AC+CE).
∴点F在射线CF上运动(CF是∠ACB的角平分线),
当点E与D重合时,CF=![]() (AC+CD)=2
(AC+CD)=2![]() ,
,
当点E与B重合时,CF=![]() (AC+CB)=
(AC+CB)=![]() ,
,
∵![]() -2
-2![]() =
=![]() ,
,
∴点F的运动的路径长为![]() .
.
故答案为:![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目