Question

【题目】定义：点关于原点的对称点为，以为边作等边，则称点为的“等边对称点”；

（1）若，求点的“等边对称点”的坐标；

（2）若点是双曲线上动点，当点的“等边对称点”点在第四象限时，

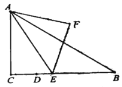
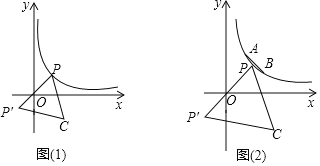
①如图（1），请问点是否也会在某一函数图象上运动？如果是，请求出此函数的解析式；如果不是，请说明理由；

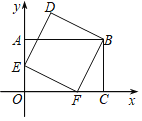
②如图（2），已知点，，点是线段上的动点，点在轴上，若以、、、这四个点为顶点的四边形是平行四边形时，求点的纵坐标的取值范围.

Answer 1

【答案】（1）或；（2）①；②或

【解析】

（1）根据P点坐标得出P'的坐标，可求PP'=4；设C（m，n），有PC=P'C=24，通过解方程即可得出结论；

（2）①设P（c，），得出P'的坐标，利用连点间的距离公式可求的长，设C（s，t），有，然后通过解方程可得，再根据消元c即可得xy=-6；

②分AG为平行四边形的边和AG为平行四边形的对角线两种情况进行分类讨论．

解：（1）∵P（1，），
∴P'（-1，-），
∴PP'=4，
设C（m，n），
∴等边△PP′C，
∴PC=P'C=4，

解得n=或-，
∴m=-3或m=3．
如图1，观察点C位于第四象限，则C（，-3）．即点P的“等边对称点”的坐标是（，-3）．

（2）①设，∴，

∴，

设，

，

∴，

∴，

∴，

∴，

∴或，

∴点在第四象限，，

∴，

令，

∴，即；

②已知，，则直线为，设点，设点，，即，，，构成平行四边形，点在线段上，；

当为对角线时，平行四边形对角坐标之和相等；

，，，即；

当为边时，平行四边形，

，，，即；

当为边时，平行四边形，

，，，而点在第三象限，，即此时点不存在；

综上，或.