题目内容
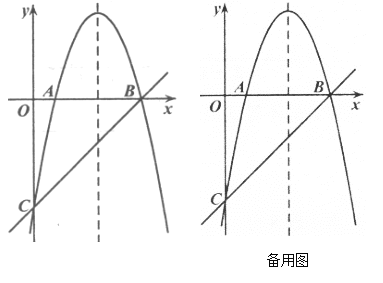
【题目】如图,抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
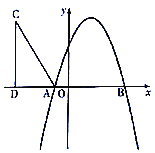
(1)求抛物线的解析式;
(2)在第二象限内取一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,连接
,连接![]() ,且
,且![]() ,
,![]() ,将
,将![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位,当点
个单位,当点![]() 落在抛物线上时,求
落在抛物线上时,求![]() 的值;
的值;
(3)在(2)的条件下,当点![]() 第一次落在抛物线上时记为点
第一次落在抛物线上时记为点![]() ,点
,点![]() 是抛物线对称轴上一点.试探究:在抛物线上是否存在点
是抛物线对称轴上一点.试探究:在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或9;(3)存在,
或9;(3)存在,![]() 或
或![]() 或
或![]() ,理由见解析
,理由见解析
【解析】
(1)由![]() 的坐标,利用待定系数法可求得抛物线的解析式;
的坐标,利用待定系数法可求得抛物线的解析式;
(2)根据题意可求得![]() 点坐标,设平移后的点
点坐标,设平移后的点![]() 的对应点为
的对应点为![]() ,则
,则![]() 点的纵坐标为
点的纵坐标为![]() ,代入抛物线解析式可求得
,代入抛物线解析式可求得![]() 点的坐标,则可求得平移的单位,可求得
点的坐标,则可求得平移的单位,可求得![]() 的值;
的值;
(3)由(2)可求得E点坐标,连接![]() 交对称轴于点
交对称轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,当
,当![]() 为平行四边形的边时,过
为平行四边形的边时,过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,则可证得
,则可证得![]() ,可求得
,可求得![]() ,即可求得
,即可求得![]() 到对称轴的距离,则可求得
到对称轴的距离,则可求得![]() 点的横坐标,代入抛物线解析式可求得
点的横坐标,代入抛物线解析式可求得![]() 点坐标;当
点坐标;当![]() 为对角线时,由
为对角线时,由![]() 的坐标可求得线段
的坐标可求得线段![]() 的中点坐标,设
的中点坐标,设![]() ,由
,由![]() 点的横坐标则可求得
点的横坐标则可求得![]() 点的横坐标,代入抛物线解析式可求得
点的横坐标,代入抛物线解析式可求得![]() 点的坐标.
点的坐标.
(1)![]()
(2)![]() ,且
,且![]() ,∴
,∴![]() 且
且![]() ,∴
,∴![]()
设平移后点![]() 的对应点
的对应点![]() 、
、![]() ,则
,则![]() 、
、![]() 点的纵坐标为8
点的纵坐标为8
代入抛物线得![]() ∴
∴![]() ,
,![]()
∴![]() 或
或![]()
∵![]() ,∴当点
,∴当点![]() 落在抛物线上时,向右平移了7或9个单位
落在抛物线上时,向右平移了7或9个单位
∴![]() 或9
或9
(3)∵抛物线对称轴为![]()
∴可设![]() ,由(2)可知
,由(2)可知![]()
①当![]() 为平行四边形的边时,连接
为平行四边形的边时,连接![]() 交对称轴于
交对称轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]()
当![]() 为平行四边形的边时,过
为平行四边形的边时,过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,如图
,如图
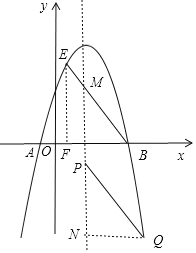
则![]()
可知![]() ,∴
,∴![]()
设![]() ,则
,则![]()
∴![]() ,
,![]() 或
或![]()
∴![]() 或
或![]()
②当![]() 为对角线时
为对角线时
∵![]() ,
,![]()
∴线段![]() 的中点
的中点![]() ,则
,则![]() 的中点为
的中点为![]()
设![]() ,且
,且![]()
∴![]() ,得
,得![]()
把![]() 代人抛物线可得
代人抛物线可得![]()
∴![]()
∴![]() 或
或![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目