题目内容
 如图所示,AB∥CD,∠D=2∠B,设AD=a,DC=b,那么线段AB的长为
如图所示,AB∥CD,∠D=2∠B,设AD=a,DC=b,那么线段AB的长为
- A.2a-b
- B.2b-a
- C.a+b
- D.

C
分析:先过点C作CE∥AD交AB于点E,把梯形分成一个平行四边形和三角形,再利用平行四边形和平行线的性质得AD=CE=BE=a,CD=AE=b,即可求出AB=AE+BE=a+b.
解答: 解:过点C作CE∥AD交AB于点E,
解:过点C作CE∥AD交AB于点E,
∴∠CEB=∠A,
∵CD∥AB,
∴∠A+∠ADC=180°,
CE=AD=a,CD=AE=b,
∵∠CEB+∠B+∠BCE=180°,
∴∠ADC=∠B+∠BCE,
∵∠ADC=2∠B,
∴2∠B=∠B+∠BCE,
∴∠B=∠BCE,
∴CE=BE=a,
∴AB=BE+AE=a+b.
故选C.
点评:本题主要考查了学生对梯形的性质和梯形的辅助线的作法,然后利用平行四边形和平行线的性质即可求出结果.
分析:先过点C作CE∥AD交AB于点E,把梯形分成一个平行四边形和三角形,再利用平行四边形和平行线的性质得AD=CE=BE=a,CD=AE=b,即可求出AB=AE+BE=a+b.
解答:
 解:过点C作CE∥AD交AB于点E,
解:过点C作CE∥AD交AB于点E,∴∠CEB=∠A,
∵CD∥AB,
∴∠A+∠ADC=180°,
CE=AD=a,CD=AE=b,
∵∠CEB+∠B+∠BCE=180°,
∴∠ADC=∠B+∠BCE,
∵∠ADC=2∠B,
∴2∠B=∠B+∠BCE,
∴∠B=∠BCE,
∴CE=BE=a,
∴AB=BE+AE=a+b.
故选C.
点评:本题主要考查了学生对梯形的性质和梯形的辅助线的作法,然后利用平行四边形和平行线的性质即可求出结果.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )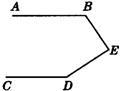 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=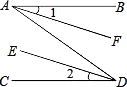 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=