��Ŀ����
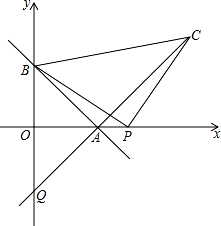
��֪����ͼ��һ�κ��� y=kx+b �� x �ᡢy ��ֱ��ڵ� A �͵� B��A ������Ϊ��3��0������OAB=45�㣮
��1����һ�κ����ı���ʽ��
�� P �� x ����������һ�㣬�� P Ϊֱ�Ƕ��㣬BP Ϊ���ڵ�һ������������ Rt��BPC������ CA ���� ���� y ���ڵ� Q��
������ P ������Ϊ��4��0������� C �����꣬�����ֱ�� AC �ĺ�������ʽ��
�ڵ� P ���� x ���������˶�ʱ��Q ���λ���Ƿ����仯�������䣬������������ꣻ����仯�� ��������ı仯��Χ��
�����㡿һ�κ����ۺ��⣮
����������1��������AOB=90�㣬��OAB=45�㣬�ɵ���OBA=��OAB=45�㣬�� OA=OB���� A��3��0���� �ɵ� B��0��3�������� y=kx+b �ɵó� k��b ��ֵ�����ɵó�һ�κ����ı���ʽ��
�ٹ��� C �� x ��Ĵ��ߣ�����Ϊ D����֤��BOP�ա�PDC�������ó��� P��C�������꣬���� A��C
��Ĵ��ߣ�����Ϊ D����֤��BOP�ա�PDC�������ó��� P��C�������꣬���� A��C
��������� y=k1x+b1 ��⼴�ɣ�
������BOP�ա�PDC���ɵ� PD=BO��CD=PO�����߶ι�ϵ�����ó� OA=OB���ó� AD=CD���ɽ� �Ĺ�ϵ�ɵ���AOQ �ǵ���ֱ�������Σ��ɵó� OQ=OA�����ɵó��� Q �����꣮
����𡿽⣺��1���ߡ�AOB=90�㣬��OAB=45��
���OBA=��OAB=45�㣬
��OA=OB��
��A��3��0����
��B��0��3����
�� 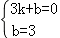 ��
��
��� k=��1��
��y=��x+3��
����ͼ������ C �� x ��Ĵ��ߣ�����Ϊ D��
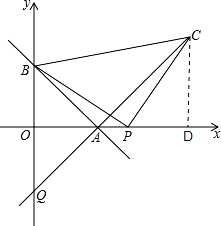
�ߡ�BPO+��CPD=��PCD+��CPD=90�㣬
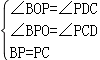 ���BPO=��PCD�� ����BOP ����PDC ��
���BPO=��PCD�� ����BOP ����PDC ��
��
����BOP�ա�PDC��AAS����
��PD=BO=3��CD=PO��
��P��4��0����
��CD=PO=4���� OD=3+4=7��
���� C��7��4����
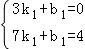 ��ֱ�� AC �ĺ�����ϵʽΪ y=k1x+b1�� �� ��
��ֱ�� AC �ĺ�����ϵʽΪ y=k1x+b1�� �� ��
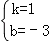 ��� ��
��� ��
��ֱ�� AC �ĺ�����ϵʽΪ y=x��3��
�ڵ� Q ��λ�ò������仯��
�ɢ�֪��BOP�ա�PDC������ P �� x ���������˶�ʱ��������BOP�ա�PDC��
��PD=BO��CD=PO��
��PO+PD=CD+OB���� OA+AD=OB+CD��
����OA=OB��
��AD=CD��
���CAD=45�㣬
���CAD=��QAO=45�㣬
��OQ=OA=3��
���� Q ��������0����3����

 �߽�������ϵ�д�
�߽�������ϵ�д�ij��ȥˮ�������г��ɹ�ƻ������������ A��B ����ƻ����������ƻ��Ʒ��һ�������ۼ۶�Ϊ 6 Ԫ/ǧ�ˣ������۸�����ͬ��A �ҹ涨���������������� 1000 ǧ�ˣ������ۼ۵� 92%�Żݣ������� �������� 2000 ǧ�ˣ������ۼ۵� 90%�Żݣ����� 2000 ǧ�˵İ����ۼ۵� 88%�Żݣ�B �ҵĹ涨�� �±���
| ������Χ��ǧ�ˣ� | 0��500 | 500 ���ϡ�1500 | 1500 ���ϡ�2500 | 2500 ���� |
| �� ��Ԫ�� | ���ۼ۵� 95% | ���ۼ۵� 85% | ���ۼ۵� 75% | ���ۼ۵� 70% |
[����˵���������۸�ֶμ��㣬�磺ij������ƻ�� 2100 ǧ�ˣ����ܷ���
=6��95%��500+6��85%��1000+6��75%��
��1����������� 600 ǧ��ƻ���������� A ��������Ҫ Ԫ���� B ��������Ҫ Ԫ�� ��������� x ǧ��ƻ����1500��x��2000���������� A ��������Ҫ Ԫ���� B ��������Ҫ
Ԫ���ú� x �Ĵ���ʽ��ʾ����
��3��������Ҫ���� 1800 ǧ��ƻ�������ܰ�����ѡ�����ļ��������Ż�����˵�����ɣ�
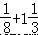 ��2.75��������24����
��2.75��������24����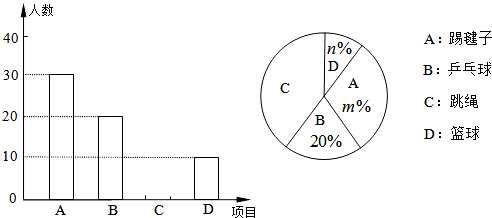
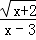 ���Ա��� x ��ȡֵ��Χ��
���Ա��� x ��ȡֵ��Χ�� 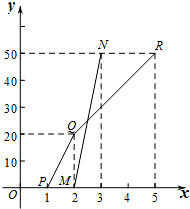
 �У�
�� ��
�� ����
���� �Ķ����ǣ� ��.
�Ķ����ǣ� ��. B��
B�� C��
C�� D��
D��
