题目内容

等腰直角三角形的外接圆半径等于

A.
腰长
B.
腰长的 $数学公式$ 倍
C.
底边的 $数学公式$ 倍
D.
腰上的高

B
分析：由于等腰直角三角形的外心是斜边的中点，外接圆半径是底边的一半，可据此进行判断．
解答：∵等腰直角三角形的外接圆圆心在斜边的中点，半径等于斜边的一半；
∴设腰长是x，则斜边长是 $\text{[math]}$ x，所以外接圆半径等于 $\text{[math]}$ x，则可知等腰直角三角形的外接圆半径等于腰长的 $\text{[math]}$ 倍．
故选B．
点评：等腰直角三角形是一种常见的特殊三角形，斜边上的高、中心及顶角平分线“三线合一”；斜边中点到三顶点的距离相等，即为三角形的外心．

练习册系列答案

小学单元同步核心密卷系列答案

长江全能学案英语听力训练系列答案

随堂练习册课时练系列答案

中考整合集训系列答案

阳光课堂口算题系列答案

快乐每一天神算手天天练系列答案

小学教材全解全析系列答案

原创讲练测课优新突破系列答案

学优冲刺100系列答案

名校秘题小学毕业升学系统总复习系列答案

相关题目

一个半径为r的圆内切于一个等腰直角三角形，另一个半径为R的圆外接于这个三角形，则

等于（　　）

28、操作与探究：
（1）图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠（如图②）．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形的顶点）上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足何条件时，一定能折成组合矩形？

半径为R的圆外接于等腰直角三角形ABC，而DABC的内切圆半径为r，则大圆的周长与小圆的周长之比值为（　）

A．　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　 D．

一个半径为r的圆内切于一个等腰直角三角形，另一个半径为R的圆外接于这个三角形，则 $数学公式$ 等于

A.
$数学公式$ +1
B.
$数学公式$
C.
2
D.
3

一个半径为r的圆内切于一个等腰直角三角形，另一个半径为R的圆外接于这个三角形，则

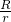等于（　　）