题目内容
一个半径为r的圆内切于一个等腰直角三角形，另一个半径为R的圆外接于这个三角形，则
等于（ ）
| R |
| r |
A．
| B．
| C．2 | D．3 |
∵等腰直角三角形内切圆的半径为r，外接圆的半径为R，
∴等腰直角三角形的三边分别为R+r，R+r，2R，
∴由勾股定理得2（R+r）2=（2R）2，
整理得（
）2-2
-1=0，
则
=1±
（舍去负号）．
故选A．
∴等腰直角三角形的三边分别为R+r，R+r，2R，
∴由勾股定理得2（R+r）2=（2R）2，
整理得（
| R |
| r |
| R |
| r |
则
| R |
| r |
| 2 |
故选A．
练习册系列答案
中考解读考点精练系列答案
相关题目
一个半径为r的圆内切于一个等腰直角三角形，另一个半径为R的圆外接于这个三角形，则
等于（ ）
| R |
| r |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
（2013•恩施州）如图所示，一半径为1的圆内切于一个圆心角为60°的扇形，则扇形的周长为
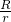等于
+1