题目内容
．
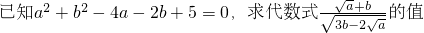解：因为a2+b2-4a-2b+5=0，
所以a2-4a+4+b2-2b+1=0，
即（a-2）2+（b-1）2=0．
（a-2）2=0，且（b-1）2=0．
所以a=2，b=1．∴原式=
=
=
=
=
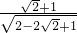
=3+2
．
分析：根据已知a2+b2-4a-2b+5=0，变形为（a-2）2+（b-1）2=0?a=2，b=1，代入代数式即可得出答案．
点评：本题考查了二次根式的化简求值，难度适中，关键是根据已知a2+b2-4a-2b+5=0变形后求出a，b的值．
所以a2-4a+4+b2-2b+1=0，
即（a-2）2+（b-1）2=0．
（a-2）2=0，且（b-1）2=0．
所以a=2，b=1．∴原式=
==
==
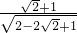
=3+2．分析：根据已知a2+b2-4a-2b+5=0，变形为（a-2）2+（b-1）2=0?a=2，b=1，代入代数式即可得出答案．
点评：本题考查了二次根式的化简求值，难度适中，关键是根据已知a2+b2-4a-2b+5=0变形后求出a，b的值．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
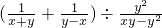，其中x=-2，y=1．
，则n=________．