题目内容
已知∠MON=45°,其内部有一点P关于OM的对称点是A,关于ON的对称点是B,且OP=2cm,则S△AOB=
2cm2
2cm2
.分析:根据轴对称的性质可得OA=OP,OB=OP,∠AOM=∠MOP,∠BON=∠BOP,然后求出∠AOB=90°,从而判断出△AOB是等腰直角三角形,根据等腰直角三角形的面积等于直角边平方的一半列式进行计算即可得解.
解答: 解:∵点P关于OM的对称点是A,
解:∵点P关于OM的对称点是A,
∴OA=OP,∠AOM=∠MOP,
∵点P关于ON的对称点是B,
∴OB=OP,∠BON=∠BOP,
∴OA=OB=OP,∠AOB=∠AOM+∠MOP+∠BON+∠BOP=2(∠MOP+∠NOP)=2∠MON=2×45°=90°,
∴△AOB是等腰直角三角形,
∵OP=2cm,
∴S△AOB=
×22=2cm2.
故答案为:2cm2.
 解:∵点P关于OM的对称点是A,
解:∵点P关于OM的对称点是A,∴OA=OP,∠AOM=∠MOP,
∵点P关于ON的对称点是B,
∴OB=OP,∠BON=∠BOP,
∴OA=OB=OP,∠AOB=∠AOM+∠MOP+∠BON+∠BOP=2(∠MOP+∠NOP)=2∠MON=2×45°=90°,
∴△AOB是等腰直角三角形,
∵OP=2cm,
∴S△AOB=
| 1 |
| 2 |
故答案为:2cm2.
点评:本题考查了轴对称的性质,等腰直角三角形的判定,熟记性质判定出△AOB是等腰直角三角形是解题的关键,作出图形更形象直观.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
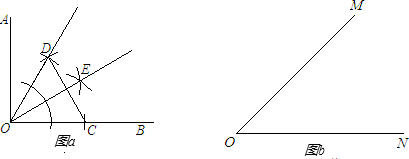
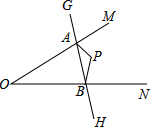 如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是
如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是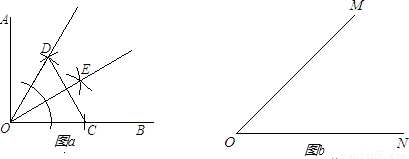
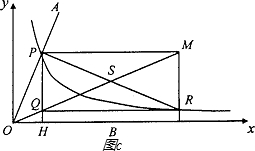
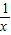 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: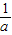 )、R(b,
)、R(b,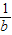 ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.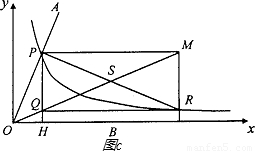

 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.