题目内容
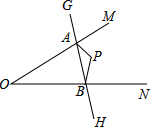 如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是
如图,已知∠MON=45°,P是∠MON内的一点,点G、H分别是P点关于MO、NO的对称点,GH与OM,ON分别相交于点A,B.已知GH=5cm,则△PAB的周长是5
5
cm.若连接GO、HO,则△GHO是等腰直角
等腰直角
三角形.分析:根据轴对称的性质可得PA=AG,PB=BH,然后求出△PAB的周长=GH;连接OP,根据轴对称的性质可得PO=GO,∠POA=∠GOA,PO=HO,∠POB=∠HOB,然后求出GO=HO,∠GOH=2∠MON=90°,从而判断出△GHO是等腰直角三角形.
解答: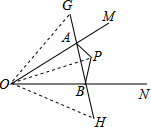 解:∵点G、H分别是P点关于MO、NO的对称点,
解:∵点G、H分别是P点关于MO、NO的对称点,
∴PA=AG,PB=BH,
∴△PAB的周长=PA+AB+PB=AG+AB+BH=GH,
∵GH=5cm,
∴△PAB的周长=5cm;
连接OP,∵点G、H分别是P点关于MO、NO的对称点,
∴PO=GO,∠POA=∠GOA,PO=HO,∠POB=∠HOB,
∴GO=HO,
∠GOH=∠GOA+∠POA+∠POB+∠HOB=2(∠POA+∠POB)=2∠MON,
∵∠MON=45°,
∴∠GOH=90°,
∴△GHO是等腰直角三角形.
故答案为:5;等腰直角.
 解:∵点G、H分别是P点关于MO、NO的对称点,
解:∵点G、H分别是P点关于MO、NO的对称点,∴PA=AG,PB=BH,
∴△PAB的周长=PA+AB+PB=AG+AB+BH=GH,
∵GH=5cm,
∴△PAB的周长=5cm;
连接OP,∵点G、H分别是P点关于MO、NO的对称点,
∴PO=GO,∠POA=∠GOA,PO=HO,∠POB=∠HOB,
∴GO=HO,
∠GOH=∠GOA+∠POA+∠POB+∠HOB=2(∠POA+∠POB)=2∠MON,
∵∠MON=45°,
∴∠GOH=90°,
∴△GHO是等腰直角三角形.
故答案为:5;等腰直角.
点评:本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,已知∠MON=90°,点A、B分别在射线OM、ON上移动,∠OAB的平分线与∠OBA的外角平分线所在直线交于点C,试猜想:随着A、B点的移动,∠ACB的大小是否变化?说明理由.
如图,已知∠MON=90°,点A、B分别在射线OM、ON上移动,∠OAB的平分线与∠OBA的外角平分线所在直线交于点C,试猜想:随着A、B点的移动,∠ACB的大小是否变化?说明理由.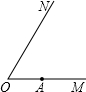 如图,已知∠MON=60°,A是射线OM上的点,OA=8.
如图,已知∠MON=60°,A是射线OM上的点,OA=8. (2012•五通桥区模拟)如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为
(2012•五通桥区模拟)如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为 如图,已知∠MON,只用直尺(没有刻度)和圆规求作:(保留作图痕迹,不要求写作法)
如图,已知∠MON,只用直尺(没有刻度)和圆规求作:(保留作图痕迹,不要求写作法) 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为