题目内容
如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).(原创)(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

解:解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴ .
.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CHO中,∠CHO=90°,∠CAD=42°,
∴CD=AD•tan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
答:二楼的层高BC约为5.8米.

练习册系列答案
相关题目
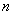 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式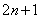 来表示.
来表示.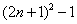 ;
; 2,x,0的平均数是0,那么这组数据的中位数是 。(
2,x,0的平均数是0,那么这组数据的中位数是 。(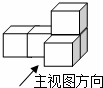
 与一次函数
与一次函数 的图象相交于点
的图象相交于点 (如图所示),则能使
(如图所示),则能使 成立的x的取值范围是_________.
成立的x的取值范围是_________. 
 中最大的数是()
中最大的数是() B、
B、 C、
C、 D、
D、
 的整数解有()
的整数解有()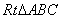 和等腰
和等腰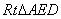 中,∠ACB=∠AED=90°,且AD=AC
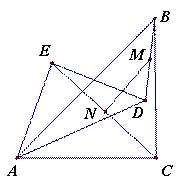
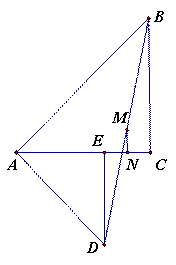
中,∠ACB=∠AED=90°,且AD=AC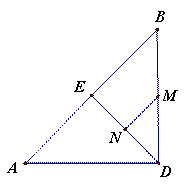 (2)探究:若把(1)小题中的△AED绕点A旋转一定角度,如图2所示,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请以逆时针旋转45°得到的图形(图3)为例给予证明位置关系成立,以顺时针旋转45°得到的图形(图4)为例给予证明数量关系成立,若不成立,请说明理由。
(2)探究:若把(1)小题中的△AED绕点A旋转一定角度,如图2所示,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请以逆时针旋转45°得到的图形(图3)为例给予证明位置关系成立,以顺时针旋转45°得到的图形(图4)为例给予证明数量关系成立,若不成立,请说明理由。