题目内容
 如图,在⊙O中D为弧AB的中点,CD为直径,弦AB交CD于P,PE⊥BC于E,BC=12,CE:EB=3:1,求AB的长.
如图,在⊙O中D为弧AB的中点,CD为直径,弦AB交CD于P,PE⊥BC于E,BC=12,CE:EB=3:1,求AB的长.分析:求出BE、CE,证△CEP∽△PEB,求出PE,根据勾股定理求出PB,代入AB=2PB求出即可.
解答:解:∵BC=12,CE:BE=3:1,
∴CE=9,BE=3,
∵在⊙O中D为弧AB的中点,CD为直径,
∴CD⊥AB,AB=2BP,
∴∠CPB=90°,
∵PE⊥CB,
∴∠PEB=∠PEC=90°,
∴∠C+∠CPE=90°,∠CPE+∠BPE=90°,
∴∠C=∠BPE,
∴△CEP∽△PEB,
∴
=
,
∴
=
,
∴PE2=27,
在Rt△PEB中,由勾股定理的:BP=
=6,
∴AB=2PB=12.
∴CE=9,BE=3,
∵在⊙O中D为弧AB的中点,CD为直径,
∴CD⊥AB,AB=2BP,
∴∠CPB=90°,
∵PE⊥CB,
∴∠PEB=∠PEC=90°,
∴∠C+∠CPE=90°,∠CPE+∠BPE=90°,
∴∠C=∠BPE,
∴△CEP∽△PEB,
∴
| PE |
| BE |
| CE |
| PE |
∴
| PE |
| 3 |
| 9 |
| PE |
∴PE2=27,
在Rt△PEB中,由勾股定理的:BP=
| 27+32 |
∴AB=2PB=12.
点评:本题考查了相似三角形的性质和判定,勾股定理和垂径定理的应用,注意:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 如图,在⊙O中,D、E分别为半径OA、OB上的点,且AD=BE.点C为弧AB上一点,连接CD、CE、CO,∠AOC=∠BOC.
如图,在⊙O中,D、E分别为半径OA、OB上的点,且AD=BE.点C为弧AB上一点,连接CD、CE、CO,∠AOC=∠BOC. 如图,在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA为半径的圆交AB于D点,若AC=6,求弧AD的长.
如图,在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA为半径的圆交AB于D点,若AC=6,求弧AD的长.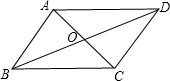 (1)如图,在?ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
(1)如图,在?ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )