题目内容
先阅读下面题目及解题过程,再根据要求回答问题.
已知:如图所示,在平行四边形ABCD中,∠A的平分线与BC相交于点E,∠B的平分线与AD边相交于点F,AE、BF相交于点O,试说明四边形ABEF是菱形.
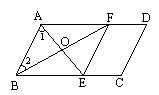
解:因为四边形ABCD是平行四边形 ①
所以AD∥BC ②
所以∠ABE+∠BAF=![]() ③
③
所以![]() ∠ABE+
∠ABE+![]() ∠BAF=
∠BAF=![]() ④
④
即∠1+∠2=![]() ⑤
⑤
所以∠AOB=![]() ⑥
⑥
所以AE⊥BF ⑦
所以四边形ABEF是菱形 ⑧
问:(1)上述说理过程是否正确?答:________________;
(2)如有错误,指出在第________步到第________步说理有误,应在第________步后添加如下说理过程:________________.
答案:
解析:
解析:
|
解:(1)上述说理过程不正确. (2)在第⑦到第⑧步说理有误,应在第⑦步后添加如下说理过程: 因为AD∥BC 所以∠EBF=∠AFB,∠EAF=∠AEB 因为∠ABF=∠EBF,∠BAE=∠FAE 所以∠ABF=∠AFB,∠BAE=∠AEB 所以AB=AF,AB=BE 所以AF=BE 又AF∥BE 所以四边形ABEF是平行四边形 所以平行四边形ABEF是菱形. |

练习册系列答案
相关题目

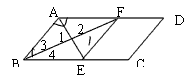
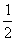 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4=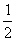 ∠ABE,
∠ABE, 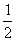 (∠BAF+∠ABE)=90。
(∠BAF+∠ABE)=90。