题目内容
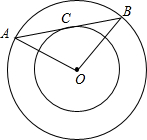如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若AB=8，圆环的面积是16π
16π
．分析：连接OC，根据切线性质得出OC⊥AB，根据垂直定理得出AC=BC=
AB=4，∠OCB=90°，由勾股定理得出OB2-OC2=BC2=16，即可求出答案．
| 1 |
| 2 |
解答：
解：连接OC，
∵AB切小⊙O于C，
∴OC⊥AB，
∴AC=BC=
AB=4，∠OCB=90°，
由勾股定理得：OB2-OC2=BC2=16，
∴圆环的面积是πOB2-πOC2=π（OB2-OC2）=16π，
故答案为：16π．
解：连接OC，
∵AB切小⊙O于C，
∴OC⊥AB，
∴AC=BC=
| 1 |
| 2 |
由勾股定理得：OB2-OC2=BC2=16，
∴圆环的面积是πOB2-πOC2=π（OB2-OC2）=16π，
故答案为：16π．
点评：此题综合运用了切线的性质定理、勾股定理，垂径定理的应用，注意：圆的切线垂直于过切点的半径．
练习册系列答案
阅读快车系列答案
相关题目
圆于点C，过点C作直线CE⊥AD，垂足为E，交大圆于F，H两点．
如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于P，如果AB=4cm，则图中阴影部分的面积为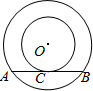
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点，若两圆的半径分别为3cm和5cm，则AB的长为
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，切点为C，若AB=