题目内容
如图,四边形ABCD中,AB∥CD,AB ≠ CD,BD = AC.
(1)求证:AD = BC;
(2)若E、F、G、H分别是AB、CD、AC、BD的中点,求证:线段EF与线段GH互相垂直平分.
 |
证明:(1)做BM∥AC,BM交DC的延长线于点M,则∠ACD =∠BMD …………1分
∵AB∥CD BM∥AC
∴四边形ABMC为平行四边形 …………………………………………………2分
∴AC = BM
∵BD = AC
 ∴BM = BD
∴BM = BD
∴∠BDM = ∠BMD
∴∠BDC = ∠ACD
在△BDC和△ACD中

∴△BDC ≌ △ACD ………………………………………………………4分
∴BC = AD ……………………………………………………………………………5分
(2)连接EG、GF、FH、HE …………………………………………………6分
∵E、H为AB、BD的中点 ∴
同理 ,
, ,
,
∵BC = AD ∴EG = FG = FH = EH …………………………………………………8分
∴四边形EGFH为菱形
∴EF与GH互相垂直平分 ………………………………………………………………9分

在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为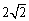 的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现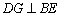 ,请你帮他说明理由.
,请你帮他说明理由.
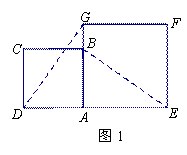 |
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
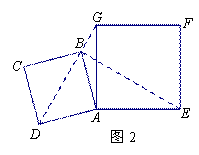 |
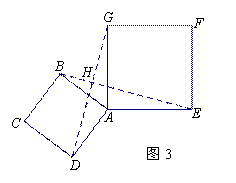
(3)如图3,若小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△ 与△
与△ 面积之和的最大值,并简要说明理由.
面积之和的最大值,并简要说明理由.
 |
 内接于
内接于 ,若四边形
,若四边形 是平行四边形,则
是平行四边形,则 的大小为 ( )
的大小为 ( ) (B)
(B) (C)
(C) (D)
(D)

 如图,某仓储中心有一斜坡AB,其坡度为
如图,某仓储中心有一斜坡AB,其坡度为 ,顶部A处的高AC为4m,B、C在同一水平地面上。
,顶部A处的高AC为4m,B、C在同一水平地面上。 面的高。
面的高。 ,结果精确到0.1m)
,结果精确到0.1m) 的图象与x轴有两个交点A
的图象与x轴有两个交点A ,B
,B ,且
,且 ,点P
,点P
 时,
时, B.当
B.当 时,
时,
 D.当
D.当
 tan
tan
 ;
; B.
B.
 D.
D.
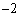 的点与原点的距离是 .
的点与原点的距离是 .