题目内容
（2011•清流县质检）（1）计算：（
+1）（
-1）-|1-tan60°|+（x10+1）0；
（2）解不等式组
，并把解集在数轴上表示出来．
| 3 |
| 3 |
（2）解不等式组
|
分析：（1）根据平方差公式，特殊角的三角函数值，绝对值的性质以及任何非0数的0次幂等于1，进行计算即可求解；
（2）先求出两个不等式的解集，再找出解集的公共部分即可．
（2）先求出两个不等式的解集，再找出解集的公共部分即可．
解答：解：（1）（
+1）（
-1）-|1-tan60°|+（x10+1）0，
=3-1-（1-
）+1，
=2-1+
+1，
=2+
；
（2）
，
解不等式①得，x＜0，
解不等式②得，x≥-1，
∴不等式组的解集是-1≤x＜0．
用数轴表示为：
| 3 |
| 3 |
=3-1-（1-
| 3 |
=2-1+
| 3 |
=2+
| 3 |
（2）
|
解不等式①得，x＜0，
解不等式②得，x≥-1，
∴不等式组的解集是-1≤x＜0．
用数轴表示为：
点评：本题考查了二次根式的混合运算，绝对值的性质，0次幂的性质，不等式组的解法，是综合题，但难度不大，计算时要注意运算符号的处理以及解集公共部分的确定．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
（2011•清流县质检）星期天，小明在解答下列题目时卡壳了．
（2011•清流县质检）如图，将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表，则an= （用含n的代数式表示）．
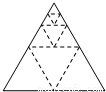
| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |