Question

【题目】在中，于点D．

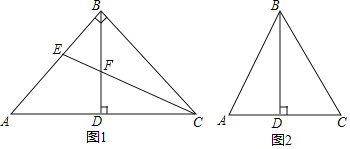
（1）如图1，当时，若CE平分，交AB于点E，交BD于点F．

①求证：是等腰三角形；

②求证：；

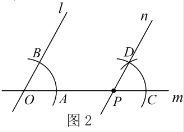
（2）点E在AB边上，连接CE．若，在图2中补全图形，判断与之间的数量关系，写出你的结论，并写出求解与关系的思路．

Answer 1

【答案】（1）①见解析；②见解析；（2），理由见解析

【解析】

（1）①根据，以及，即可得到，即可判定是等腰三角形；

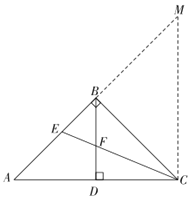
②延长AB至M，使得，连接CM，根据三角形中位线定理可得，再根据，可得，进而得出；

（2）与（1）②同理可得；由，可证明和分别是等腰三角形；由以及，可得，即可得到与之间的数量关系：．

（1）①在中，于点D，

，

，

∵CE平分，

，

，

是等腰三角形；

②如图，延长AB至M，使得，连接CM，

，

，

，

由①得，，

，

，

（2）．

求解与关系的思路：

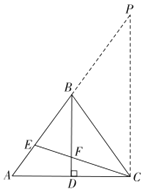
a，延长AB至P，使得，连接CP，与（1）②同理可得；

b，由，可证明和分别是等腰三角形；

c，由以及，可得，即可证明．