题目内容
如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)(5分)求证:CG是⊙O的切线;
(2)(5分)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.

【答案】
证明见解析
【解析】证明:(1)如图,连接OC,

∵AB为⊙O的直径,∴∠ACB=900。
∵在Rt△DCF中,DG=FG,∴CG=DG=FG。
∴∠CFG=∠FCG。
又∵∠CFG=∠AFE,∴∠FCG=∠AFE。
∵OA=OC,∴∠EAF=∠OCA。
又∵DE⊥AB,∴∠EAF+∠AFE=90°。 ∴∠OCA+∠FCG=90°,即∠GCO=90°。
又∵OC是⊙O的半径,∴CG为⊙O的切线。
(2)∵DG=FG,∴ 。
。
∵DC=CB,∴ ,∴
,∴ 。
。
又∵ ,∴
,∴  。∴AF=FC。
。∴AF=FC。
又∵OA=OB,∴OF是△ABC的中位线。∴OF∥BC。
(1)连接OC.欲证CG是⊙O的切线,只需证明∠CGO=90°,即CG⊥OC。
(2)根据直角三角形ABC、直角三角形DCF的面积公式,以及直角三角形斜边的中线等于斜边的一半求得AC=2AF;然后根据三角形中位线的判定和性质证得结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
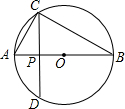 如图,点C在以AB为直径的⊙O上,CD⊥AB于P,设AP=a,PB=b.
如图,点C在以AB为直径的⊙O上,CD⊥AB于P,设AP=a,PB=b.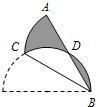 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,直径AB和弧BC交于点D,已知AB=6,则图中阴影部分的面积和周长分别等于
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,直径AB和弧BC交于点D,已知AB=6,则图中阴影部分的面积和周长分别等于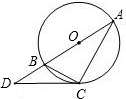 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A. (2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
(2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.