题目内容
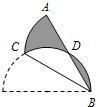 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,直径AB和弧BC交于点D,已知AB=6,则图中阴影部分的面积和周长分别等于
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,直径AB和弧BC交于点D,已知AB=6,则图中阴影部分的面积和周长分别等于分析:连CD,AC,由直径所对的圆周角为直角得到∠ACB=90°,得到∠A=60°,即△ACD为等边三角形,于是有弓形BD的面积=弓形CD的面积,阴影部分的面积=扇形DAC的面积,阴影部分的周长=半圆弧长加直径,然后根据扇形的面积公式和弧长公式计算即可.
解答:解:连CD,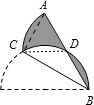 AC,如图,
AC,如图,
∵AB为直径,∠ABC=30°,
∴∠ACB=90°,∠A=60°,
∴△ACD为等边三角形,
∴∠DCB=30°,
∴弓形BD的面积=弓形CD的面积,
∴阴影部分的面积=扇形DAC的面积=
=
;
阴影部分的周长=
•2π•3+6=3π+6.
故答案为
,3π+6.
 AC,如图,
AC,如图,∵AB为直径,∠ABC=30°,
∴∠ACB=90°,∠A=60°,
∴△ACD为等边三角形,
∴∠DCB=30°,
∴弓形BD的面积=弓形CD的面积,
∴阴影部分的面积=扇形DAC的面积=
| 60•π•32 |
| 360 |
| 3π |
| 2 |
阴影部分的周长=
| 1 |
| 2 |
故答案为
| 3π |
| 2 |
点评:本题考查了扇形的面积公式和弧长公式:S=
,l=
.也考查了圆周角定理的推论和等边三角形的性质.
| nπr2 |
| 360 |
| nπr |
| 180 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
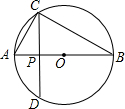 如图,点C在以AB为直径的⊙O上,CD⊥AB于P,设AP=a,PB=b.
如图,点C在以AB为直径的⊙O上,CD⊥AB于P,设AP=a,PB=b.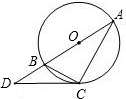 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A. (2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
(2012•黔南州)已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.