Question

20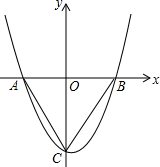．如图，抛物线y=x²-x+c与x轴交于点A（-2，0），与y轴交于点C．
（1）求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为点B，连接AC、BC，求△ABC的面积．

Answer 1

分析 （1）把A的坐标代入抛物线的解析式即可求得c的值，即可气的抛物线的解析式；
（2）求得B的坐标和C的坐标，然后利用三角形面积公式求解．

解答 解：（1）把A（-2，0）代入解析式得4+2+c=0，解得：c=-6，
则抛物线的解析式是y=x²-x-6；
（2）在y=x²-x-6中令y=0，则x2-x-6=0，
解得：x₁=3，x₂=-2．
则B的坐标是（3，0）．
则AB=3-（-2）=5，
在y═x²-x-6中，令x=0，解得y=-6，
则C的坐标是（0，-6）．
则S_△ABC=$\frac{1}{2}$×5×6=15．

点评 本题考查了待定系数法求抛物线的解析式，正确求得A和B的坐标是关键．