题目内容
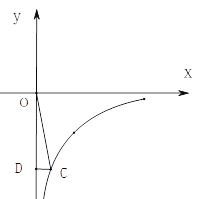
【题目】如图，点C在反比例函数y=
的图象上，过点C作CD⊥y轴，交y轴负半轴于点D，且△ODC的面积是3．
（1）求反比例函数y=
的解析式；
（2）若CD=1，求直线OC的解析式．
【答案】（1）y=
（2）y=﹣6x
【解析】试题分析：（1）设C点坐标为（x，y），根据k的几何意义得到|k|=2×3=6，而图象在第四象限，则k=﹣6；
（2）由于CD=1，则点C （ 1，y ），利用反比例函数解析式确定C点坐标，然后根据待定系数法求直线OC的解析式．
试题解析：解：（1）设C点坐标为（x，y）．∵△ODC的面积是3，∴ 
ODDC=
x（﹣y）=3，∴xy=﹣6，而xy=k，∴k=﹣6，∴所求反比例函数解析式为
；
（2）∵CD=1，即点C （ 1，y ），把x=1代入
，得y=﹣6，∴C 点坐标为（1，﹣6），设直线OC的解析式为y=mx，把C （1，﹣6）代入y=mx得﹣6=m，∴直线OC的解析式为：y=﹣6x．
练习册系列答案
名校课堂系列答案
相关题目
【题目】列一元一次方程解应用题：
某水果店计划购进
.
两种水果，下表是.这两种水果的进货价格：
水果品种 |
|
|
进货价格（元 |
|
|
（1）若该水果店要花费
元同时购进两种水果共
，则购进.两种水果各为多少
？
（2）若水果店将种水果的售价定为
元
，要使购进的这批水果在完全售出后达到
的利润率，种水果的售价应该定为多少？
