题目内容
如图，已知
ABCD，∠A=45°，AD=4，以AD为直径的半圆O与
BC相切于点B，则图中阴影部分的面积为
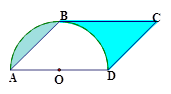
ABCD，∠A=45°，AD=4，以AD为直径的半圆O与BC相切于点B，则图中阴影部分的面积为
A．4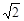 | B．π+2 | C．4 | D．2 |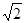
C
连接BD，OB，
∵AD为圆O的直角，
∴∠ABD=90°又∠A=45°，
∴△ABD为等腰直角三角形，又O为AD的中点，
∴BO⊥AD，且BO=
AD=2，AB=BD，
∵扇形AOB与扇形OBD的圆心角都为90°，半径都为2，
得到S扇形AOB=S扇形OBD，又S△AOB=S△DOB
∴S弓形AB=S弓形BD，
由ABCD为平行四边形，得到AD=BC，
则S阴影=S△BCD=BC?BO=AD?OB=×4×2=4．
故选C．
∵AD为圆O的直角，
∴∠ABD=90°又∠A=45°，
∴△ABD为等腰直角三角形，又O为AD的中点，
∴BO⊥AD，且BO=
AD=2，AB=BD，∵扇形AOB与扇形OBD的圆心角都为90°，半径都为2，
得到S扇形AOB=S扇形OBD，又S△AOB=S△DOB
∴S弓形AB=S弓形BD，
由ABCD为平行四边形，得到AD=BC，
则S阴影=S△BCD=
BC?BO=AD?OB=×4×2=4．故选C．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
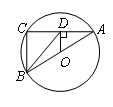
中，直径CD⊥弦AB,且
，则
的度数是 。
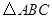内接于⊙O，
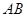是非直径的弦，∠CAE＝∠B．
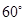的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将三角形ABC沿OE方向平移，使得点B与点E重合为止．设∠POF＝
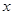°，则
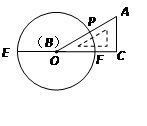
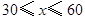
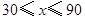
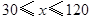
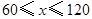
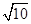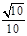cm
cm