Question

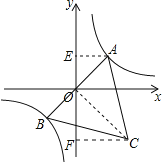
【题目】如图，已知等边三角形的顶点分别在反比例函数图像的两个分支上，点在反比例函数的图像上，当的面积最小时，的值__________．

Answer 1

【答案】-3

【解析】

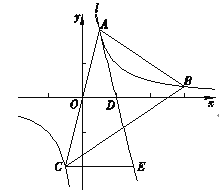
当等边三角形ABC的边长最小时，△ABC的面积最小，点A，B分别在反比例函数y=图象的两个分支上，则当A、B在直线y=x上时最短，即此时△ABC的面积最小，根据反比例函数图象的对称性可得OA=OB，设OA=x，则AC=2x，OC=x，根据等边三角形三线合一可证明△AOE∽△OCF，根据相似三角形面积比等于相似比的平方可得结论．

解：根据题意当A、B在直线y=x上时，△ABC的面积最小，

函数y=图象关于原点对称，

∴OA=OB，

连接OC，过A作AE⊥y轴于E，过C作CF⊥y轴于F，

∵△ABC是等边三角形，

∴AO⊥OC，

∴∠AOC=90°，∠ACO=30°，

∴∠AOE+∠COF=90°，

设OA=x，则AC=2x，OC=x，

∵AE⊥y轴，CF⊥y轴，

∴∠AEO=∠OFC=∠AOE+∠OAE=90°，

∴∠COF=∠OAE，

∴△AOE∽△OCF，

∴，

∵顶点A在函数y=图象的分支上，

∴S△AOE=，

∴S△OCF=，

∵点C在反比例函数y=（k≠0）的图象上，

∴k=-3，

故答案为-3．