题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 经过
经过![]() ,
,![]() 两点,交
两点,交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() ,且
,且![]() .
.
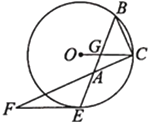
(1)求证:![]() ;
;
(2)设![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)5
【解析】
(1)连结![]() ,有切线的性质和平行线的性质,得
,有切线的性质和平行线的性质,得![]() ,由圆周角定理
,由圆周角定理![]() ,根据等腰三角形的性质,即可求解;
,根据等腰三角形的性质,即可求解;
(2)过点G作GM⊥AC于点M,由平行线的性质得∠OCF=∠F,设GM=3x,则CM=4x,CG=5x,结合等腰直角三角形的性质,列出关于x的方程,求出x的值,即可得到答案.
(1)连结![]() ,
,
∵![]() 与
与![]() 相切,
相切,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)过点G作GM⊥AC于点M,
∵![]() ,
,
∴∠OCF=∠F,
∴sin∠OCF=![]() ,
,
设GM=3x,则CM=4x,CG=5x,
∵![]() ,
,
∴ABC和AMG是等腰直角三角形,
∴AC=BC=7,AM=GM=3x,
∴3x+4x=7,解得:x=1,
∴![]() .
.


练习册系列答案
相关题目